[3D Transform/03] Euler Angles, Axis-Angle Rotation
Introduction
앞선 포스트에서는 3차원 공간에 존재하는 어떠한 점(point)이나 벡터(vector)는 어떤 좌표계(coordinate system)에서 보는지에 따라 다른 좌표(coordinate)를 가지고 있음을 살펴보았습니다. 그리고 좌표계간 상관관계를 이용해 변환 행렬을 구해봤는데요. 이를 통해 획득한 $\mathbf{R}$(rotation matrix), $\mathbf{t}$(translation vector), 그리고 $\mathbf{T}$(transformation matrix)는 머리로는 이해되나 가슴으로는 잘 이해가 되지 않을 것입니다. 특히 회전과 관련된 성분들은 최종 결과물만 보고서 도대체 이 행렬은 얼마나 회전시키는 녀석인지, 아니면 이게 회전 행렬은 맞는지 한눈에 알아볼 방법이 없습니다. 즉, 직관적이지 않죠.
오늘은 3차원에서의 행렬을 직관적으로 표현하기 위해 제안된 두 표기법에 대해 소개하려 합니다. 오일러 각(Euler angles)과 Rodriguez rotation이라고도 불리는 Axis-Angle rotation에 대해서 다룰 예정입니다. 그러나 이 두 방법은 모두 각자의 사정에 의해 표준처럼 자리 잡지는 않았습니다. 그렇기에 이번 포스트에서는 간략하게 저 방법들이 어떤 것인지 소개하고, 다음 포스트에서는 사원수(quarternion)에 대해 이야기할 예정입니다.
Euler Angles
오일러 각의 알파이자 오메가는 회전을 쪼개서 생각하는 것입니다. 3차원의 회전을 한 번에 이해하려 하지 말고, 세 개의 축에 대한 회전의 중첩으로 이해하자는 제안입니다.
$$\mathbf{R \to R_x, R_y, R_z}$$
이를 이해하면 자연스레 드는 의문이 있습니다. 이런 식으로 나누면, 회전 순서에 따라 다른 결과가 나오는 거 아니야? 맞습니다. 오일러 각에서는 회전의 순서가 굉장히 중요한데요. 어떤 축을 먼저 회전시키는지에 따라 각 축에 대해 같은 회전각을 가지고 다른 결과를 얻을 수 있습니다. 이에 따라 오일러 각을 사용할 때는 어떤 순서로 회전을 주었는지를 표기해 주어야 합니다.
그러나 순서에 대한 표기가 생략된 오일러 각을 많이 접할 수 있는데요. 이 경우 업계 표준처럼 사용되는 yaw-pitch-roll 회전이라고 간주할 수 있습니다. 이는 항공 공학에서 사용되는 좌표계로, 쉽게 말하면 $ZYX$ 순서로 회전을 한다는 의미입니다. 아래 그림은 yaw-pitch-roll 좌표계에 대한 그림이며, 각각에 대한 변환 행렬을 정리해 봤습니다.

- yaw (Z 축으로 $\alpha$만큼 회전)
$$ \begin{bmatrix}
cos\alpha & -sin\alpha & 0 \\
sin\alpha & cos\alpha & 0 \\
0 & 0 & 1 \\
\end{bmatrix}$$
- pitch (Y 축으로 $\beta$만큼 회전)
$$ \begin{bmatrix}
cos\beta & 0 & sin\beta \\
0 & 1 & 0 \\
-sin\beta & 0 & cos\beta \\
\end{bmatrix}$$
- roll (X 축으로 $\gamma$만큼 회전)
$$ \begin{bmatrix}
1 & 0 & 0 \\
0 & cos\gamma & -sin\gamma \\
0 & sin\gamma & cos\gamma \\
\end{bmatrix}$$
Euler Angles의 한계
오일러 각은 굉장히 직관적이라는 큰 장점이 있지만 잘 사용되지는 않습니다. 장점을 상쇄할 만큼 큰 단점들이 있는데요. 짐벌 락(Gimbal lock)과 회전각에 대해 interpolation이 되지 않는다는 문제가 있습니다.
우선 짐벌 락은 오일러 각을 통해 회전을 하게 되는 경우 어느 축이든 $\pm 90^\circ $ 회전을 하게 되면, 축이 겹치게 됩니다. 이로 인해 DOF가 3에서 2로 줄게 되고, 회전 표현에 제약이 생기게 됩니다. 실제로 아폴로 11호가 이 짐벌 락 문제로 인해 자세 제어에 어려움을 겪었다고 하네요. 짐벌 락은 singularity problem이라고도 부르니 알고 계시면 좋을 것 같네요.
여기에 추가로 오일러 각에서 2개 이상의 축을 사용해 회전을 하게 되는 경우 linear interpolation을 통해 회전 변환을 부드럽게 표현할 수 없습니다. 실제로 파워포인트 등에서 애니메이션 효과를 주게 된다면, 단순히 2D 회전을 하게 되면 부드럽게 효과가 적용되는 것을 볼 수 있지만, 3차원으로 회전 효과를 적용하면 영상이 끊기는 것을 볼 수 있습니다.
이 두 문제에 집중해 개선한 방법이 Axis-Angle 회전(rotation vector)인데요. 아래에서 간단하게 살펴보도록 하겠습니다.
Axis-Angle Rotation (Rotation vector)
축-각 회전(Axis-Angle rotation)은 오일러 각의 짐벌 락과 interpolation 제약 등을 어느 정도 해결했습니다. 그 이름에서도 직관적으로 알 수 있듯이 회전 변환을 회전축과 회전각을 이용해 표현한 방법인데요. 최종적으로 벡터 형태로 표현되기에 rotation vector로 불리기도 합니다. 또한, 처음 제안한 Rodrigues's rotation formula로 유도할 수 있어 로드리게스 회전이라고 부르기도 합니다.
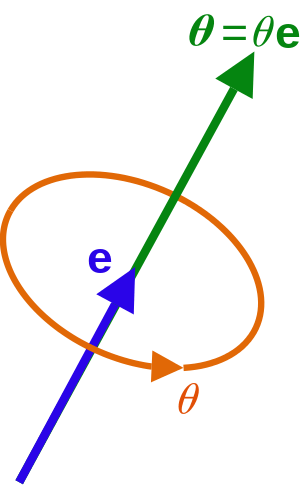
회전축을 나타내는 단위 벡터 $\mathbf{e}$와 회전각 $\theta$가 있을 때, 회전 벡터 $\mathbf{\theta}$는 방향은 $\mathbf{e}$, 크기는 $\theta$인 벡터($\mathbf{\theta}=\theta\mathbf{e}$)가 됩니다. 물리적 특징을 살펴보면, 임의의 축에 직교하는 평면에 대한 모든 회전을 표현할 수 있게 됩니다. 단일 벡터로 회전을 표현해 순서를 신경 쓸 필요가 없으며 짐벌 락에 빠질 위험도 적습니다 (없지는 않습니다).
그러나 Axis-Angle roation의 경우 연산량이 너무 방대해 회전이 중첩되는 경우 여러 트릭을 사용해야지 계산이 가능하다는 문제가 있습니다. 그래서 실전에서는 회전 벡터보다는 사원수(quarternion)를 많이 사용하고 있습니다. 따라서 복잡한 회전 벡터의 유도 과정은 잘 정리되어 있는 블로그 포스팅 소개로 대체하고자 하며, 결괏값을 소개하며 그 안에 내포된 의미를 살펴보고자 합니다.
$$\mathbf{R}=cos\theta \mathbf{I} + (1-cos\theta)\mathbf{nn}^T+sin\theta \mathbf{n}^{\wedge}$$
여기서 역으로 회전각 $\theta$를 유도하는 방법은 Axis-Angle rotation의 대각 성분의 합(trace, $tr$)을 통해 구할 수 있습니다.
$$tr(\mathbf{R})=cos\theta \ tr(\mathbf{I}) + (1-cos\theta)\ tr(\mathbf{nn}^T)+sin\theta \ tr(\mathbf{n}^{\wedge})$$
$$=3cos\theta + (1-cos\theta)=1+2cos\theta$$
$$\therefore \theta=arccos(\frac{tr(\mathbf{R})-1}{2})$$
위 식에서 $3 \times 3$ 단위 행렬($\mathbf{I}$)의 trace는 3이며, $\mathbf{nn}^T$의 경우 단위 벡터의 자기 자신과의 내적이기 때문에 1로 변하게 됩니다. 거기에 반대칭 행렬(skew-symmetric matrix)인 $\mathbf{n}^{\wedge}$의 경우 대각 성분의 합이 0입니다.
추가로, 회전축 $\mathbf{n}$은 회전 변환 후에도 아무것도 변하지 않게 됩니다. 즉, 아래와 같은 관계가 성립되게 되는데요.
$$\mathbf{Rn=n}$$
이 경우 $\mathbf{n}$이 $\mathbf{R}$의 eigen vector이며, eigen value는 1 임을 알 수 있습니다. 즉, 회전 벡터가 주어질 때 eigen decomposition 후 normalization 과정을 거치면 회전축을 구할 수 있게 됩니다.
Reference
모든 이미지에 대한 출처는 해당 이미지를 클릭하시면 열리도록 했습니다.
GitHub - gaoxiang12/slambook-en: The English version of 14 lectures on visual SLAM.
The English version of 14 lectures on visual SLAM. - GitHub - gaoxiang12/slambook-en: The English version of 14 lectures on visual SLAM.
github.com