Introduction
이전 포스트에서 설명한 것처럼, 카메라는 움직임에 따라 크기와 모양이 달라지지 않는 강체(rigid body)입니다. 그래서 SLAM에서의 3D 변환은 회전(rotation)과 평행 이동(translation)만 고려합니다.
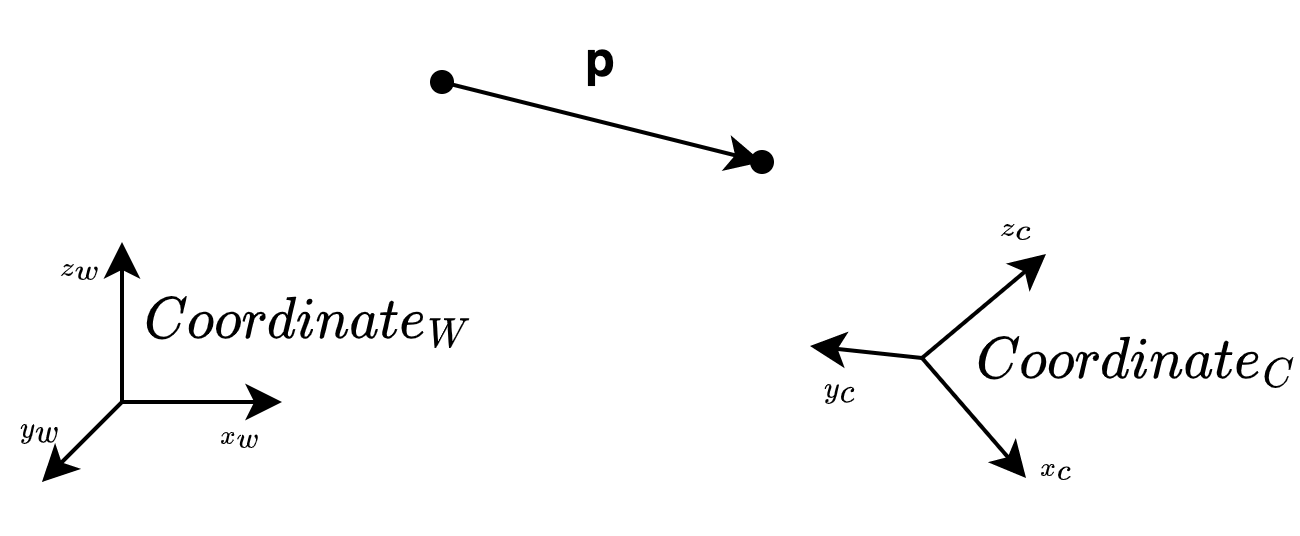
여기에 추가로 앞서 좌표계(coordinate system)에 대해서 다뤘습니다. 점(point)이나 벡터(vector)를 어느 좌표계에서 바라보는지에 따라 좌표(coordinate)가 달라지게 됩니다. SLAM에서 필수적으로 다루게 될 World coordinate과 Camera coordinate을 예시로 들어보겠습니다. 벡터 $\mathbf{p}$에 대해 World 좌표계에서 본 $\mathbf{p_w}$와 Camera 좌표계에서 본 $\mathbf{p_c}$가 존재합니다.
$$ \mathbf{p}=[x_w, y_w, z_w]\begin{bmatrix}
p_{wx} \\
p_{wy} \\p_{wz}
\end{bmatrix}, \quad\quad \mathbf{p_w}=(p_{wx},p_{wy},p_{wz})$$
$$ \mathbf{p}=[x_c, y_c, z_c]\begin{bmatrix}
p_{cx} \\
p_{cy} \\p_{cz}
\end{bmatrix}, \quad\quad \mathbf{p_c}=(p_{cx},p_{cy},p_{cz})$$
이때 우리가 궁금한 것은 $\mathbf{p_w, p_c}$ 사이의 관계입니다. 둘 사이는 어떠한 변환식이 존재할 것이며, 그 해를 변환 행렬 $\mathbf{T}$라고 정의하도록 하겠습니다. SLAM에서는 이러한 변환 행렬을 구하는 것이 주요 과제이며, 순서는 주어진 image를 가지고 실제 3차원 공간 상의 object 위치를 구하는 $\mathbf{p_c} \to \mathbf{p_w}$인 $\mathbf{T}$를 찾아야 합니다. 이번 포스트에서는 변환 행렬의 실체와 구하는 방법에 대해 이야기하도록 하겠습니다.
Rotation Matrix 유도
우선 강체 변환의 두 요소인 회전과 이동 중 회전만 있다고 가정해 봅시다. 두 좌표계(coordinate system)가 회전 변환 관계에 있다고 하면, 기저 벡터(base) 사이에 $\mathbf{(e_1,e_2,e_3)\overset{R}{\rightarrow}(e_1',e_2',e_3')}$ 관계가 성립합니다. 벡터 $\mathbf{a}$를 두 좌표계에서 바라본 좌표는 각각 $(a_1, a_2, a_3), (a_1', a_2', a_3')$이라고 하겠습니다. 벡터는 실제로는 유일하기 때문에 아래와 같은 식을 만들 수 있는데요.
$$\mathbf{a=[e_1,e_2,e_3]\begin{bmatrix}a_1 \\a_2 \\a_3
\end{bmatrix}=[e_1',e_2',e_3']\begin{bmatrix}a_1' \\a_2' \\a_3'\end{bmatrix}}$$
이제 양변에 $\begin{bmatrix} \mathbf{e_1}^T \\ \mathbf{e_2}^T \\ \mathbf{e_3}^T \end{bmatrix}$를 곱해 식을 간단하게 정리하겠습니다.
$$\underbrace{\begin{bmatrix}
\mathbf{e_1}^T\mathbf{e_1} & \mathbf{e_1}^T\mathbf{e_2} & \mathbf{e_1}^T\mathbf{e_3} \\
\mathbf{e_2}^T\mathbf{e_1} & \mathbf{e_2}^T\mathbf{e_2} & \mathbf{e_2}^T\mathbf{e_3} \\
\mathbf{e_3}^T\mathbf{e_1} & \mathbf{e_3}^T\mathbf{e_2} & \mathbf{e_3}^T\mathbf{e_3} \\
\end{bmatrix}}_I \begin{bmatrix}
a_1 \\
a_2 \\a_3
\end{bmatrix} = \underbrace{\begin{bmatrix}
\mathbf{e_1}^T\mathbf{e_1'} & \mathbf{e_1}^T\mathbf{e_2'} & \mathbf{e_1}^T\mathbf{e_3'} \\
\mathbf{e_2}^T\mathbf{e_1'} & \mathbf{e_2}^T\mathbf{e_2'} & \mathbf{e_2}^T\mathbf{e_3'} \\
\mathbf{e_3}^T\mathbf{e_1'} & \mathbf{e_3}^T\mathbf{e_2'} & \mathbf{e_3}^T\mathbf{e_3'} \\
\end{bmatrix}}_{rotation\ matrix} \begin{bmatrix}
a_1' \\
a_2' \\a_3'
\end{bmatrix} = \mathbf{Ra'}$$
기저 벡터들끼리는 서로 직교(orthogonal)한다고 가정이 들어가 있는데요. 이 경우 자기 자신과의 내적은 1, 아닌 경우는 0으로 결괏값이 매우 간단해집니다. 최종적으로 좌측은 대각 성분만 1인 단위행렬(identity matrix)이 되는 것을 볼 수 있습니다. 그렇기에 회전 전 좌표계에서의 좌표$(a_1,a_2,a_3)$와 회전 후 좌표계에서의 좌표$(a_1',a_2',a_3')$의 관계를 나타내는 변환 행렬을 회전 행렬(rotation matrix)로 간주할 수 있습니다.
결론적으로 두 좌표계의 회전 변환을 설명해 주는 rotation matrix는 변환 전과 후의 두 base matrix의 내적(하나는 전치 행렬(transpose matrix) 형태)을 계산함으로써 구할 수 있습니다. 기저 벡터들은 모두 단위 벡터(unit vector)들이며 크기가 1인 특징이 있습니다. 이로 인해 내적의 결괏값은 두 기저 벡터의 사잇각의 $cosine$ 값과 같습니다. 이런 특정 때문에 회전 행렬을 direction cosine matrix라고도 부릅니다.
Rotation Matrix 성질
회전 행렬은 $det(\mathbf{R})=1$을 만족하는 orthogonal matrix입니다. 반대로 말하면, 이를 만족하는 모든 행렬은 모두 회전 행렬이라고 할 수 있습니다. 이런 행렬들의 집합(group)을 SO(n)이라고 하는데요. Special orthogonal group의 약어로 3차원의 경우 SO(3)으로 표기합니다. 이번 포스트에서는 맛보기로 정의만 소개하고, 후에 Lie Group & Algebra를 소개하면서 자세히 다루도록 하겠습니다.
$$SO(n)=\left\{\mathbf{R}\in \mathbb{R}^{n \times n}|\mathbf{RR}^T=\mathbf{I},det(\mathbf{R})=1 \right\}$$
추가로, 회전 행렬이 orthogonal matrix의 성질을 만족하기 때문에 그 역행렬은 음의(반대) 방향으로의 회전 행렬을 나타냅니다 ($\mathbf{R^{-1}=R}^T$).
$$\mathbf{a=Ra'} \quad \to \quad \mathbf{R^{-1}a=R^T a=a'}$$
Translation Vector
행렬 계산으로 표현되는 회전과 달리 평행 이동은 결괏값에 벡터를 더해주게 됩니다. 일반적으로 회전과 평행 이동을 모두 포함한 강체 변환은 아래와 같이 표현됩니다.
$$\mathbf{a_1=Ra_2+t}$$
여기서 $\mathbf{R,t}$는 $\mathbf{a \to a'}$을 나타내는 행렬과 벡터인데요. 사실 그 물리적 의미가 조금 다릅니다. 회전 행렬(rotation matrix)은 위에서 살펴보았듯 $system_2 \to system_1$을 나타내게 됩니다. 반면에 평행 이동(translation) 벡터는 조금 다른 의미를 갖고 있습니다. 두 좌표계의 원점을 각각 $O_1, O_2$라고 했을 때, translation vector는 $\overrightarrow{O_1O_2}$와 같습니다. 어떻게 본다면 $system_2 \to system_1$처럼 이해될 수 있지만, $vector_2 \to vector_1$로 이해하는 게 편할 듯합니다.
하나 더 짚고 넘어갈 부분은 translation vector의 역은 $\mathbf{-t}$가 아닙니다. 만약 회전이 없는 순수한 평행 이동 변환이라면 문제없겠지만, 회전이 섞이는 순간 문제는 좀 더 복잡해집니다. 역변환을 구하기 위해 위 식을 정리하면 아래와 같으며, translation vector의 역은 $\mathbf{-R}^T\mathbf{t}$임을 알 수 있습니다.
$$\mathbf{R^{-1}(a_1-t)=R}^T\mathbf{(a_1-t)=a_2}$$
Transformation Matrix
위에서 구한 일반적인 강체 변환이 중첩되면 어떻게 될까요? 위 식의 가장 큰 문제는 비선형(non-linear) 구조를 띈다는 점입니다. 변환이 중첩된다면 계산은 매우 복잡해지게 됩니다. 아래는 변환이 두 번만 중첩된 경우입니다.
$$\mathbf{a''=R_2(R_1 a+t_1)+t_2}$$
이 식을 선형 시스템(linear system)으로 끌고 오기 위해서 약간의 트릭을 쓰게 되는데요. 위 변환들을 homogeneous coordinates으로 표현해 $4 \times 4$ Transformation Matrix($\mathbf{T}$)를 생성하게 됩니다. 이로서 3D 강체 변환을 선형 변환으로 표현하게 되었고, 중첩에 대해서도 변환 행렬을 여러 번 내적함으로써 계산을 단순화하였습니다.
$$\begin{bmatrix}
\mathbf{a'} \\ 1
\end{bmatrix}=\begin{bmatrix}
\mathbf{R} & \mathbf{t} \\
0^T & 1 \\
\end{bmatrix}\begin{bmatrix}
\mathbf{a} \\ 1
\end{bmatrix}=\mathbf{T}\begin{bmatrix}
\mathbf{a} \\ 1
\end{bmatrix}$$
이를 만족하는 $\mathbf{T}$들이 속한 집합을 SE(3)라고 부릅니다. 이는 special euclidean group의 약어로, 자세한 설명은 Lie Group & Algebra를 설명하며 다루도록 하겠습니다. SE(3)군에 대한 정의는 아래와 같으며, 회전 행렬과 같이 역행렬이 역변환을 나타냅니다. 이는 translation vector가 단독으로 사용되는 경우 상상하기 힘든 일입니다.
$$SE(3)=\left\{ \mathbf{T}=\begin{bmatrix}
\mathbf{R} & \mathbf{t} \\
0^T & 1 \\
\end{bmatrix} \in \mathbb{R}^{4 \times 4}|\mathbf{R} \in SO(3),\mathbf{t} \in \mathbb{R}^3 \right\}$$
$$\mathbf{T}^{-1}=\begin{bmatrix}
\mathbf{R}^T & -\mathbf{R}^T \mathbf{t} \\
0^T & 1 \\
\end{bmatrix}$$
Reference
GitHub - gaoxiang12/slambook-en: The English version of 14 lectures on visual SLAM.
The English version of 14 lectures on visual SLAM. - GitHub - gaoxiang12/slambook-en: The English version of 14 lectures on visual SLAM.
github.com
Introduction
이전 포스트에서 설명한 것처럼, 카메라는 움직임에 따라 크기와 모양이 달라지지 않는 강체(rigid body)입니다. 그래서 SLAM에서의 3D 변환은 회전(rotation)과 평행 이동(translation)만 고려합니다.
여기에 추가로 앞서 좌표계(coordinate system)에 대해서 다뤘습니다. 점(point)이나 벡터(vector)를 어느 좌표계에서 바라보는지에 따라 좌표(coordinate)가 달라지게 됩니다. SLAM에서 필수적으로 다루게 될 World coordinate과 Camera coordinate을 예시로 들어보겠습니다. 벡터

이때 우리가 궁금한 것은
Rotation Matrix 유도
우선 강체 변환의 두 요소인 회전과 이동 중 회전만 있다고 가정해 봅시다. 두 좌표계(coordinate system)가 회전 변환 관계에 있다고 하면, 기저 벡터(base) 사이에
이제 양변에
기저 벡터들끼리는 서로 직교(orthogonal)한다고 가정이 들어가 있는데요. 이 경우 자기 자신과의 내적은 1, 아닌 경우는 0으로 결괏값이 매우 간단해집니다. 최종적으로 좌측은 대각 성분만 1인 단위행렬(identity matrix)이 되는 것을 볼 수 있습니다. 그렇기에 회전 전 좌표계에서의 좌표
결론적으로 두 좌표계의 회전 변환을 설명해 주는 rotation matrix는 변환 전과 후의 두 base matrix의 내적(하나는 전치 행렬(transpose matrix) 형태)을 계산함으로써 구할 수 있습니다. 기저 벡터들은 모두 단위 벡터(unit vector)들이며 크기가 1인 특징이 있습니다. 이로 인해 내적의 결괏값은 두 기저 벡터의 사잇각의
Rotation Matrix 성질
회전 행렬은
추가로, 회전 행렬이 orthogonal matrix의 성질을 만족하기 때문에 그 역행렬은 음의(반대) 방향으로의 회전 행렬을 나타냅니다 (
Translation Vector
행렬 계산으로 표현되는 회전과 달리 평행 이동은 결괏값에 벡터를 더해주게 됩니다. 일반적으로 회전과 평행 이동을 모두 포함한 강체 변환은 아래와 같이 표현됩니다.
여기서
하나 더 짚고 넘어갈 부분은 translation vector의 역은
Transformation Matrix
위에서 구한 일반적인 강체 변환이 중첩되면 어떻게 될까요? 위 식의 가장 큰 문제는 비선형(non-linear) 구조를 띈다는 점입니다. 변환이 중첩된다면 계산은 매우 복잡해지게 됩니다. 아래는 변환이 두 번만 중첩된 경우입니다.
이 식을 선형 시스템(linear system)으로 끌고 오기 위해서 약간의 트릭을 쓰게 되는데요. 위 변환들을 homogeneous coordinates으로 표현해
이를 만족하는
Reference
GitHub - gaoxiang12/slambook-en: The English version of 14 lectures on visual SLAM.
The English version of 14 lectures on visual SLAM. - GitHub - gaoxiang12/slambook-en: The English version of 14 lectures on visual SLAM.
github.com
