Introduction
앞선 포스트에서는 회전을 직관적으로 표현할 수 있는 Euler Angle과 Axis-Angle Rotation에 대해 다뤘습니다. 하지만 직관적인 대신 Euler angle은 Gimbal lock, Axis-Angle rotation은 높은 연산량으로 인해 실시간이며 높은 정확도를 요구하는 SLAM에서는 실제 적용이 어렵습니다.
이런 문제를 해결하기 위해 벡터의 등장과 함께 거의 사장되었던 사원수(Quaternion)가 재조명되었는데, 이는 벡터의 등장 이전에 3차원을 표현하기 위해 제안된 방식이었습니다. 사원수의 성질 자체는 매우 간단하지만, 회전과 무슨 관계가 있길래 사용하는지 그 원리에 대한 이해는 꽤 어렵습니다. 하지만 이를 모르면 사원수는 단순히 회전을 표현하기 위해 끼워 맞춘 개념이 되며, 단순 암기처럼 느껴지게 됩니다.
이번 포스트에서는 사원수가 어떻게 3차원 회전을 표현할 수 있는지를 시작으로 그 성질을 다루도록 하겠습니다. 이미 해당 내용을 모두 알고 있거나, 단순히 사용법만 궁금하신 경우 아래 사원수와 3차원 회전 장을 보시면 됩니다.
Imaginary number
$$\mathbf{q} = q_0 + q_1i + q_2j + q_3k$$
사원수는 기본적으로 위와 같이 복소수(complex number)의 형태를 띠고 있습니다. 엄밀히 말하면 애매한 부분이 있지만 개념을 이해하는데 중요하지는 않으니 넘어가도록 하겠습니다. 실수부와 허수부를 구분해서 볼 때, 회전에 대한 단서는 어디에 있을까요? 기본적으로 실수가 회전을 온전히 나타내기에는 많은 제약이 존재한다는 점을 기억하면, 허수부에 우리가 찾는 회전에 대한 단서가 있음을 유추할 수 있습니다.
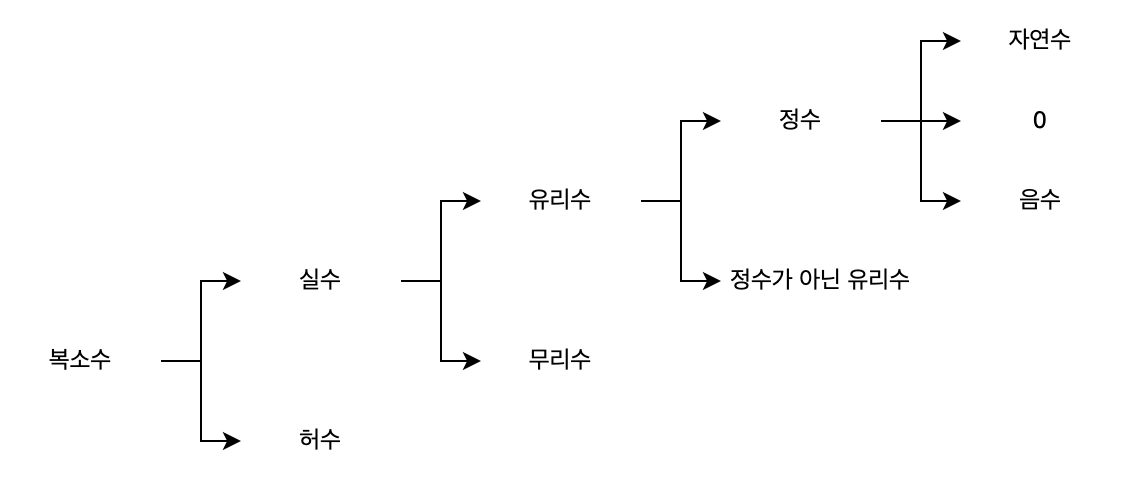
수의 체계는 아마도 자연수에서 시작했을 것입니다. 부족원이나 가족의 인원을 세기 위해 자연수의 개념이 어렴풋이 등장하지 않았을까 생각해 봅니다. 그리고 이러한 자연수는 0차원, 즉 점으로 표현할 수 있습니다. 사과 반쪽 등을 따지기 시작하며 유리수 개념이 확장되었을 것입니다. 이렇듯 수는 설명 가능하게 확장되어 왔습니다. 또한, 사칙연산을 통해 차원을 0차원에서 양의 1차원으로 확장시킬 수 있었죠.
이러한 발전을 거치던 중 음수가 발견됩니다. 여태까지의 발전 방향과 다르게 음수는 일반적이지 않습니다. 즉, 직관적으로 이해할 수 없습니다. 여기서 음수를 양수끼리의 뺄셈과 혼동하면 안 됩니다. 음수의 물리적 의미는 여태까지의 자연수, 유리수 등과 다르게 양이나 크기로 설명이 불가능합니다. 이제는 방향의 개념이 추가됩니다. -1을 곱하는 행위는 반대 방향을 나타내게 되었습니다. 여기서 표현된 반대 방향은 다른 용어로 180$^\circ$ 회전과 같습니다. 지금부터는 수는 단순히 크기를 나타내는 것이 아닌 크기와 방향으로 확장되었습니다. 그러나 여전히 직선으로 표현되는 1차원을 유지하고 있죠.
자, 그러면 하나만 물어보겠습니다. 90$^\circ$ 회전을 표현할 수 있나요? 직선 상에서 90$^\circ$ 회전을 표현할 방법은 없습니다. 이제는 더 이상 1차원에 갇혀있을 수 없다는 뜻이죠. 크기는 유지하며 방향이 달라짐을 표현할 수 있도록 새로운 축이 필요해졌습니다. 허수의 등장입니다.
$$i^2=-1$$
위 식은 허수를 처음 접하면 무조건 보게되는 허수의 정의이자 성질입니다. 위 식은 어디에서 나온 것일까요? 공교롭게도 90$^\circ$ 회전을 두 번 하게 되면 180$^\circ$ 회전을 하게 됩니다. 즉, 두 번 곱하면 180$^\circ$ 회전(-1)을 나타내는 90$^\circ$ 회전의 표기법이 허수 $i$인 것을 알 수 있습니다.
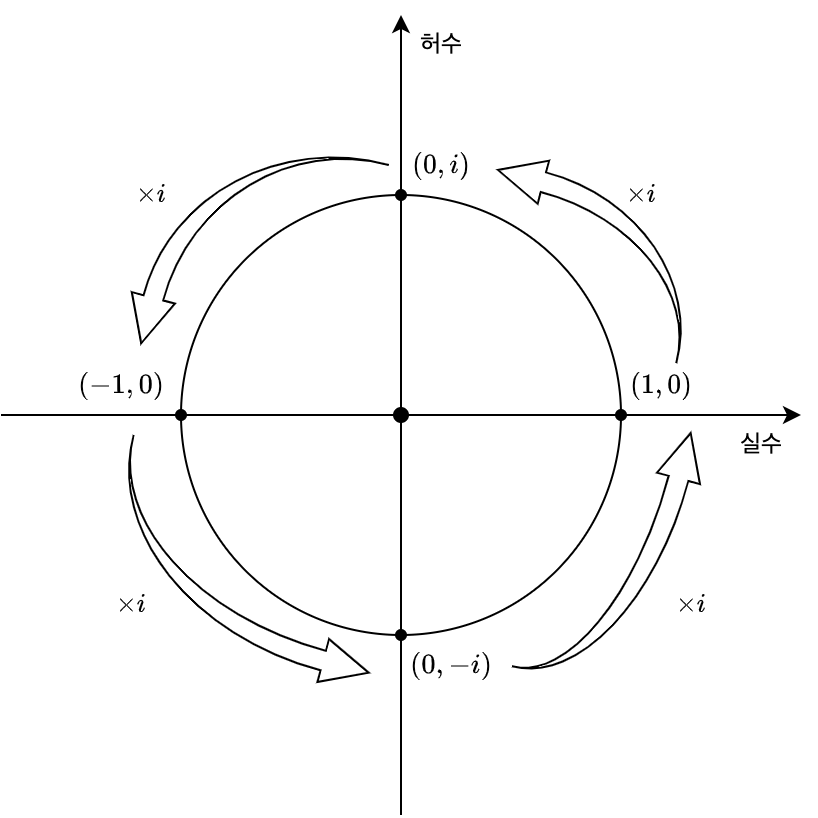
이제 허수가 회전과 관련이 있다는 것을 알게 되었습니다. 다음 장에서는 2차원에서의 회전을 허수(방향)와 실수(크기)의 조합으로 나타내보도록 하겠습니다.
2D Rotation by Complex Number
이제 기존의 실수 체계에서 회전을 표현하는 것은 꽤나 어려운 일임을 알게 되었습니다. 이를 해결하기 위해 상상 속의 수, 허수를 도입하게 되었음 역시 알게 되었죠. 바로 3차원의 회전을 표현하기 위해 도입된 사원수로 넘어가기에는 부담스럽기 때문에 우리가 잘 알고 있는 2차원 회전 변환 행렬을 복소수를 이용해 유도해 보도록 하겠습니다. 보통 삼각 함수를 통해 유도하는 회전 행렬을 복소수를 이용해 유도하게 되면 허수가 회전과 관련이 있음을 간접적으로 증명한다고 우길 수 있습니다. 우선 사전 지식으로 오일러 공식(Euler formula)을 알고 있어야 합니다.
$$e^{i \theta}=cos\ \theta + i\ sin\ \theta$$
오일러 공식은 세상에서 가장 아름다운 식으로도 불리는데요. 사실 전 이유를 잘 모르겠지만 그렇다네요. 아무튼 2차원 회전은 변환 전 좌표에 $e^{i \theta}$를 곱해줌으로서 구할 수 있습니다. 오일러 공식에 대한 유도 및 증명은 위 링크를 통해 대체하도록 하겠습니다. 본론으로 돌아와 복소수 평면의 점 $(x,\ y)$는 $x+yi$로 표현할 수 있으며, 여기에 $\theta$만큼의 회전 변환을 하기 위해 $e^{i\theta}$를 곱해주도록 하겠습니다. 추가로, 전자공학에서는 보통 전류를 $i$로 표기해 허수의 경우 $j$를 주로 사용합니다. 저는 전자공학도이기 때문에 이를 존중해 지금부터는 $i$ 대신 $j$로 표기하도록 하겠습니다.
$$e^{j\theta}(x+jy)=(cos\ \theta + j\ sin\ \theta)(x+jy)$$
$$=x\ cos\ \theta + yj\ cos\ \theta + xj\ sin\ \theta - y\ sin\ \theta$$
위 식을 실수부($x'$)와 허수부($y'$)로 구분해 표기하면 아래와 같습니다.
$$\left\{\begin{matrix}
x'=x\ cos\ \theta - y\ sin\ \theta\\y'=x\ sin\ \theta + y\ cos\ \theta
\end{matrix}\right.$$
이를 행렬의 곱으로 표현하면 아래와 같으며, 2차원 회전 변환 행렬식과 같음을 알 수 있죠.
$$\binom{x'}{y'}=\underbrace{\begin{pmatrix}
cos\ \theta & -sin\ \theta \\
sin\ \theta & cos\ \theta \\
\end{pmatrix}}_{rotation\ matrix} \binom{x}{y}$$
참고로 오일러 공식과 복소수 평면을 이용하면 극좌표계와 직각 좌표계를 자유자재로 이동할 수 있다는 사실 역시 유추할 수 있습니다.
Quaternion
이제 본격적으로 사원수(quaternion)에 대해 소개하도록 하겠습니다. 윌리엄 해밀턴(William Hamilton)에 의해 발견된 사원수는 그 이름을 따 해밀턴 수라고도 불립니다.
$$\mathbf{q} = q_0 + q_1i + q_2j + q_3k$$
사원수는 1개의 실수부와 3개의 허수부로 구성된 복소수입니다. 이때 3개의 허수부를 벡터로 묶어 표현하기도 합니다. 2차원 회전을 표기하기 위해 제안된 허수와의 가장 큰 차이점은 단연 축이 3개라는 점일 텐데요. 2차원 회전을 표현하기 위해서 1개의 허수부가 필요했던 것과 비교해, 3차원에서는 2개가 아닌 3개의 허수부가 필요합니다. (2개만 사용하면 생기는 문제는 여기서 확인하실 수 있습니다.)
그 이유에 대해서는 확실치 않지만 저는 개인적으로 회전축 정의와 관련이 있다고 생각합니다. 2차원에서의 회전은 고정된 실수축($x$축)과 허수축($y$축)에 대해서 각도를 지정해 주었습니다. 그렇기에 각도만 정의되면 회전을 나타낼 수 있었습니다. 반면에 3차원에서의 회전은 회전축에 대한 정의가 필요하며, 이는 세 개의 기저(base)를 필요로 합니다. 각도와 세 개의 축을 표현하기 위해서는 4개의 기저가 필요한 거죠.
다시 사원수로 돌아와 그 성질을 살펴보도록 하겠습니다. 허수는 자기 자신과 곱하면 -1이 되는 정의 및 성질이 있었는데요. 사원수 역시 그 특성을 계승하며, 사원수만의 독특한 성질을 갖고 있습니다. 우선 기저들의 곱을 아래 표로 살펴보도록 하겠습니다.
| $\times$ | $1$ | $i$ | $j$ | $k$ |
| $1$ | $1$ | $i$ | $j$ | $k$ |
| $i$ | $i$ | $-1$ | $k$ | $-j$ |
| $j$ | $j$ | $-k$ | $-1$ | $i$ |
| $k$ | $k$ | $j$ | $-i$ | $-1$ |
주의해서 볼 점은 교환 법칙이 성립하지 않는 점입니다. 교환을 하게 될 경우 부호가 바뀌게 되죠. 이는 물리적으로 보면 3차원에서의 벡터의 외적과 관련이 있어 보입니다. 외적은 오른손/왼손 법칙 관계 없이 교환을 하게될 경우 반대 방향을 가리키게 되죠.
분배 법칙과 결합 법칙은 성립하니 혼동하지 않으면 합니다. 여기에 추가적으로 세 기저의 곱 역시 -1이 되며, (실수부, 벡터부) 순서로 표현하는 사원수를 Hamilton quaternion이라고 합니다.
$$\mathbf{q}=[s,\mathbf{v}]^T, \quad s=q_0 \in \mathbb{R},\quad \mathbf{v}=[q_1,q_2,q_3]^T \in \mathbb{R}^3$$
$$ijk=-1$$
추가로, 사원수에서 실수부가 0인 케이스를 imaginary(or pure) quaternion이라고 하며, 반대로 허수부가 0인 경우 real quaternion이라고 합니다. 그리고 크기가 1인 사원수를 unit quaternion이라고 하며 이를 이용해 회전을 표현하니 잘 알아두시길 바랍니다.
Operations of Quaternion
이제 사원수의 연산을 정리하고 3차원 회전으로 넘어가도록 하겠습니다. 별도의 증명은 생략하고 3차원 회전 유도에 필요한 결론만 정리하도록 하겠습니다. 두 사원수 $\mathbf{p,q}$가 아래와 같을 때 각각의 연산은 다음과 같습니다.
$$\mathbf{p}=a+bi+cj+dk=[s_p, \mathbf{v_p}]^T,\quad \mathbf{q}=e+fi+gj+hk=[s_q,\mathbf{v_q}]^T$$
Addition and Subtraction
사원수의 덧셈과 뺄셈은 일반적인 복소수 계산과 같습니다. 실수부는 실수부끼리, 허수부는 허수부끼리 수행해 줍니다.
$$\mathbf{p \pm q}=(a \pm e)+(b \pm f)i+(c \pm g)j+(d \pm h)k=[s_p \pm s_q, \mathbf{v_p \pm v_q}]^T$$
Multiplication
$$\mathbf{pq}=[s_p s_q - \mathbf{v_p^T v_q}, s_p \mathbf{v_q} + s_q \mathbf{v_p} + \mathbf{v_p \times v_q}]^T$$
$$s\mathbf{q}=[ss_q, s\mathbf{v_q}]^T$$
Length (Norm)
$$||\mathbf{q}||=\sqrt{a^2+b^2+c^2+d^2}, \quad ||\mathbf{pq}||=\mathbf{||p||\ ||q||}$$
Conjugate
$$\mathbf{\bar{q}}=a-bi-cj-dk=[s_q, -\mathbf{v_q}]^T, \quad \mathbf{\bar{q}q=q\bar{q}}=[s_q^2+\mathbf{v^T v, 0}]^T$$
Inverse & Identity
$$\mathbf{q^{-1}=\bar{q}/||q||^2}, \quad \mathbf{qq^{-1}=q^{-1}q=1}$$
$$Real\ quaternion\ I=(1,0,0,0),\quad \mathbf{q}\cdot I = I\cdot\mathbf{q=q}$$
Quaternion and 3D Rotation
앞서 2차원 회전과 허수의 연관성을 보이기 위해 오일러 공식을 사용했습니다. 오일러 공식을 만족하는 복소수를 통해 삼각함수를 이용해 유도한 회전 행렬을 도출할 수 있다면 허수로 회전을 표현할 수 있음을 간접적으로 보였었죠. 이번 장에서는 이와 비슷하게 3차원 회전과 사원수의 관계를 유도하기 위해 오일러 공식을 사용할 것입니다. 오일러 공식을 만족하는 사원수를 통해 앞선 포스트에서 3차원 회전을 표현하기 위해 사용한 Angle-Axis rotation 식을 유도할 것입니다.
우선 오일러 공식을 만족하는 크기가 1인 단위 사원수는 아래와 같이 표현할 수 있습니다.
$$q = e^{\vec{u}\alpha} = \cos \frac{\alpha}{2} + \vec{u} \sin \frac{\alpha}{2}$$
이때 3차원 좌표 $\vec{v}$를 회전축(rotation axis) $\vec{u}$을 기준으로 $\alpha$만큼 회전시키는 식은 아래와 같습니다. 여기서 $\vec{v}$는 기존 3차원 좌표에 실수부 0을 추가해 imaginary quaternion($\vec{v}=(0,v_1,v_2,v_3)$)으로 만들어 계산하도록 합니다.
$$\vec{v}' = q \vec{v} q^{-1} = \left( \cos \frac{\alpha}{2} + \vec{u} \sin \frac{\alpha}{2} \right) \, \vec{v} \, \left( \cos \frac{\alpha}{2} - \vec{u} \sin \frac{\alpha}{2} \right)$$
사실 여기까지만 알면 사원수를 이용해 회전을 표현하는데 큰 어려움이 없습니다. 아래는 조금은 지루할 수 있는 증명 과정을 담고 있으니 관심 있으신 분만 참고해 주세요.
$$\vec{u}\vec{v} = \vec{u} \times \vec{v} - \vec{u} \cdot \vec{v}$$
$\vec{u},\ \vec{v}$ 모두 실수부가 0인 imaginary quaternion이므로 두 사원수의 곱셈 결과는 위 식과 같습니다. 이는 위에서 다룬 사원수의 곱셈에 모든 실수부에 0을 대입하면 쉽게 도출할 수 있습니다. 이걸 염두에 두고 위 식을 전개하면 아래와 같은 과정을 따라갑니다.
$$\begin{align}
\vec{v}' &= \vec{v} \cos^2 \frac{\alpha}{2} + \left(\vec{u}\vec{v} - \vec{v}\vec{u}\right) \sin \frac{\alpha}{2} \cos \frac{\alpha}{2} - \vec{u}\vec{v}\vec{u} \sin^2 \frac{\alpha}{2} \\[6pt]
&= \vec{v} \cos^2 \frac{\alpha}{2} + 2 \left(\vec{u} \times \vec{v}\right) \sin \frac{\alpha}{2} \cos \frac{\alpha}{2} - \left(\left(\vec{u} \times \vec{v}\right) - \left(\vec{u} \cdot \vec{v}\right)\right)\vec{u} \sin^2 \frac{\alpha}{2} \\[6pt]
&= \vec{v} \cos^2 \frac{\alpha}{2} + 2 \left(\vec{u} \times \vec{v}\right) \sin \frac{\alpha}{2} \cos \frac{\alpha}{2} - \left(\left(\vec{u} \times \vec{v}\right)\vec{u} - \left(\vec{u} \cdot \vec{v}\right)\vec{u}\right) \sin^2 \frac{\alpha}{2} \\[6pt]
&= \vec{v} \cos^2 \frac{\alpha}{2} + 2 \left(\vec{u} \times \vec{v}\right) \sin \frac{\alpha}{2} \cos \frac{\alpha}{2} - \left(\left(\left(\vec{u} \times \vec{v}\right) \times \vec{u} - \left(\vec{u} \times \vec{v}\right) \cdot \vec{u}\right) - \left(\vec{u} \cdot \vec{v}\right)\vec{u}\right) \sin^2 \frac{\alpha}{2} \\[6pt]
&= \vec{v} \cos^2 \frac{\alpha}{2} + 2 \left(\vec{u} \times \vec{v}\right) \sin \frac{\alpha}{2} \cos \frac{\alpha}{2} - \left(\left(\vec{v} - \left(\vec{u} \cdot \vec{v}\right)\vec{u}\right) - 0 - \left(\vec{u} \cdot \vec{v}\right)\vec{u}\right) \sin^2 \frac{\alpha}{2} \\[6pt]
&= \vec{v} \cos^2 \frac{\alpha}{2} + 2 \left(\vec{u} \times \vec{v}\right) \sin \frac{\alpha}{2} \cos \frac{\alpha}{2} - \left(\vec{v} - 2 \vec{u} \left(\vec{u} \cdot \vec{v}\right)\right) \sin^2 \frac{\alpha}{2} \\[6pt]
&= \vec{v} \cos^2 \frac{\alpha}{2} + 2 \left(\vec{u} \times \vec{v}\right) \sin \frac{\alpha}{2} \cos \frac{\alpha}{2} + \left(2 \vec{u} \left(\vec{u} \cdot \vec{v}\right) - \vec{v}\right) \sin^2 \frac{\alpha}{2} \\[6pt]
\end{align}$$
어디서 많이 익숙한 형태가 나오기 시작합니다. Angle-Axis rotation을 표현하기 위해 사용한 로드리게스 공식과 비슷한 형태를 띠게 되는데요. $\vec{v}$를 $\vec{u}$와 수직인 $\vec{v}_{\bot}$와 평행한 $\vec{v}_{\|}$로 나누어 표현하면 다음과 같습니다.
$$\vec{v} = \vec{v}_{\bot} + \vec{v}_{\|},\quad \vec{u} \left(\vec{u} \cdot \vec{v}\right) = \vec{v}_{\|}$$
$$\begin{align}
\vec{v}' &= \vec{v} \cos^2 \frac{\alpha}{2} + 2 \left(\vec{u} \times \vec{v}\right) \sin \frac{\alpha}{2} \cos \frac{\alpha}{2} + \left(2 \vec{u} \left(\vec{u} \cdot \vec{v}\right) - \vec{v}\right) \sin^2 \frac{\alpha}{2} \\[6pt]
&= \left(\vec{v}_{\|} + \vec{v}_{\bot}\right) \cos^2 \frac{\alpha}{2} + 2 \left(\vec{u} \times \vec{v}\right) \sin \frac{\alpha}{2} \cos \frac{\alpha}{2} + \left(\vec{v}_{\|} - \vec{v}_{\bot}\right) \sin^2 \frac{\alpha}{2} \\[6pt]
&= \vec{v}_{\|} \left(\cos^2 \frac{\alpha}{2} + \sin^2 \frac{\alpha}{2}\right) + \left(\vec{u} \times \vec{v}\right) \left(2 \sin \frac{\alpha}{2} \cos \frac{\alpha}{2}\right) + \vec{v}_{\bot} \left(\cos^2 \frac{\alpha}{2} - \sin^2 \frac{\alpha}{2}\right) \\[6pt]
&= \vec{v}_{\|} \left(\cos^2 \frac{\alpha}{2} + \sin^2 \frac{\alpha}{2}\right) + \left(\vec{u} \times \vec{v}\right) \left(2 \sin \frac{\alpha}{2} \cos \frac{\alpha}{2}\right) + \vec{v}_{\bot} \left(\cos^2 \frac{\alpha}{2} - \sin^2 \frac{\alpha}{2}\right) \\[6pt]
&= \vec{v}_{\|} + \left(\vec{u} \times \vec{v}\right) \sin \alpha + \vec{v}_\bot \cos \alpha
\end{align}$$
이는 $\vec{u}$를 기준으로 $\alpha$만큼 회전시킨 결과와 같고, 이로서 사원수를 통해 3차원 회전을 표현할 수 있음을 우길 수 있게 되었습니다. 참고로 사원수를 통한 회전식은 로드리게스 회전과 괘를 같이 합니다. 그렇기에 사원수를 로드리게스 회전을 간편하게 인코딩(encoding)하는 방법이라고도 소개하기도 합니다.
추가로 회전을 표현한 사원수 $\mathbf{q}=[q_0,q_1,q_2,q_3]^T$이 주어졌을 때, 다른 회전 행렬로 변환하기 위해서 각도와 회전축을 알아야 하는 경우가 있는데요. 이는 아래와 같은 방법으로 간단하게 구할 수 있습니다.
$$\left\{\begin{matrix}
\theta=2\ \textrm{arccos}q_0 \\ [n_x,n_y,n_z]^T=[q_1,q_2,q_3]^T/\textrm{sin}\frac{\theta}{2}
\end{matrix}\right.$$
Conclusion
이상으로 사원수와 3차원 회전에 대한 포스트를 끝내려고 합니다. 사실 이번 포스트를 기획하면서 생각했던 모든 내용을 담지는 못했는데요. 대표적으로 특장점 중 하나인 구면선형보간(Slerp)이 있습니다. 간단히 설명하면 사원수는 기존 오일러 회전이 해결하지 못한 회전의 interpolation을 해결했는데요. 이 방법이 Slerp입니다. 또한, 사원수를 통해 자연스럽게 $SO(3)$와 $so(3)$를 소개하려 했으나 아직 저도 이해가 완벽하지 않고, 내용이 너무 길어지면 지루해질 것이 우려되어 추후 Lie Group과 Lie Algebra를 소개할 때 다룰까 합니다. 저도 생소한 개념이라 이해하기에 어려움이 있었고, 글로서 풀어나가는 과정에서는 많은 좌절도 겪었는데요. 조금이라도 비슷한 어려움을 겪고 계신 분들께 도움이 되었으면 합니다. 댓글로 원하시는 주제를 적어주시면 정리해 업로드하겠습니다.
Reference
GitHub - gaoxiang12/slambook-en: The English version of 14 lectures on visual SLAM.
The English version of 14 lectures on visual SLAM. - GitHub - gaoxiang12/slambook-en: The English version of 14 lectures on visual SLAM.
github.com
Quaternions and spatial rotation - Wikipedia
From Wikipedia, the free encyclopedia Correspondence between quaternions and 3D rotations Unit quaternions, known as versors, provide a convenient mathematical notation for representing spatial orientations and rotations of elements in three dimensional sp
en.wikipedia.org