[3D Transform/03] Euler Angles, Axis-Angle Rotation

 

Introduction

---

앞선 포스트에서는 3차원 공간에 존재하는 어떠한 점(point)이나 벡터(vector)는 어떤 좌표계(coordinate system)에서 보는지에 따라 다른 좌표(coordinate)를 가지고 있음을 살펴보았습니다. 그리고 좌표계간 상관관계를 이용해 변환 행렬을 구해봤는데요. 이를 통해 획득한 $\mathbf{R}$(rotation matrix), $\mathbf{t}$(translation vector), 그리고 $\mathbf{T}$(transformation matrix)는 머리로는 이해되나 가슴으로는 잘 이해가 되지 않을 것입니다. 특히 회전과 관련된 성분들은 최종 결과물만 보고서 도대체 이 행렬은 얼마나 회전시키는 녀석인지, 아니면 이게 회전 행렬은 맞는지 한눈에 알아볼 방법이 없습니다. 즉, 직관적이지 않죠.

 

오늘은 3차원에서의 행렬을 직관적으로 표현하기 위해 제안된 두 표기법에 대해 소개하려 합니다. 오일러 각(Euler angles)과 Rodriguez rotation이라고도 불리는 Axis-Angle rotation에 대해서 다룰 예정입니다. 그러나 이 두 방법은 모두 각자의 사정에 의해 표준처럼 자리 잡지는 않았습니다. 그렇기에 이번 포스트에서는 간략하게 저 방법들이 어떤 것인지 소개하고, 다음 포스트에서는 사원수(quarternion)에 대해 이야기할 예정입니다.

 

 

Euler Angles

---

오일러 각의 알파이자 오메가는 회전을 쪼개서 생각하는 것입니다. 3차원의 회전을 한 번에 이해하려 하지 말고, 세 개의 축에 대한 회전의 중첩으로 이해하자는 제안입니다.

 

$$\mathbf{R \to R_x, R_y, R_z}$$

 

이를 이해하면 자연스레 드는 의문이 있습니다. 이런 식으로 나누면, 회전 순서에 따라 다른 결과가 나오는 거 아니야? 맞습니다. 오일러 각에서는 회전의 순서가 굉장히 중요한데요. 어떤 축을 먼저 회전시키는지에 따라 각 축에 대해 같은 회전각을 가지고 다른 결과를 얻을 수 있습니다. 이에 따라 오일러 각을 사용할 때는 어떤 순서로 회전을 주었는지를 표기해 주어야 합니다.

 

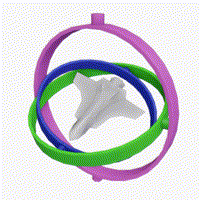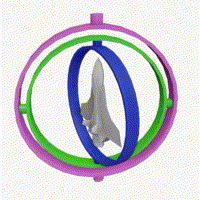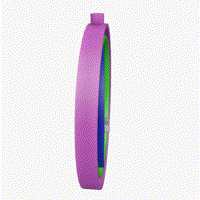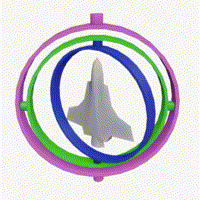
그러나 순서에 대한 표기가 생략된 오일러 각을 많이 접할 수 있는데요. 이 경우 업계 표준처럼 사용되는 yaw-pitch-roll 회전이라고 간주할 수 있습니다. 이는 항공 공학에서 사용되는 좌표계로, 쉽게 말하면 $ZYX$ 순서로 회전을 한다는 의미입니다. 아래 그림은 yaw-pitch-roll 좌표계에 대한 그림이며, 각각에 대한 변환 행렬을 정리해 봤습니다.

 

Yaw-Pitch-Roll coordinate system

 

• yaw (Z 축으로 $\alpha$만큼 회전)

$$ \begin{bmatrix}
cos\alpha & -sin\alpha & 0 \\
sin\alpha & cos\alpha & 0 \\
0 & 0 & 1 \\
\end{bmatrix}$$

• pitch (Y 축으로 $\beta$만큼 회전)

$$ \begin{bmatrix}
cos\beta & 0 & sin\beta \\
0 & 1 & 0 \\
-sin\beta & 0 & cos\beta \\
\end{bmatrix}$$

• roll (X 축으로 $\gamma$만큼 회전)

$$ \begin{bmatrix}
1 & 0 & 0 \\
0 & cos\gamma & -sin\gamma \\
0 & sin\gamma & cos\gamma \\
\end{bmatrix}$$

 

 

Euler Angles의 한계

---

오일러 각은 굉장히 직관적이라는 큰 장점이 있지만 잘 사용되지는 않습니다. 장점을 상쇄할 만큼 큰 단점들이 있는데요. 짐벌 락(Gimbal lock)과 회전각에 대해 interpolation이 되지 않는다는 문제가 있습니다.

 

우선 짐벌 락은 오일러 각을 통해 회전을 하게 되는 경우 어느 축이든 $\pm 90^\circ $ 회전을 하게 되면, 축이 겹치게 됩니다. 이로 인해 DOF가 3에서 2로 줄게 되고, 회전 표현에 제약이 생기게 됩니다. 실제로 아폴로 11호가 이 짐벌 락 문제로 인해 자세 제어에 어려움을 겪었다고 하네요. 짐벌 락은 singularity problem이라고도 부르니 알고 계시면 좋을 것 같네요.

 

Gimbal lock

 

여기에 추가로 오일러 각에서 2개 이상의 축을 사용해 회전을 하게 되는 경우 linear interpolation을 통해 회전 변환을 부드럽게 표현할 수 없습니다. 실제로 파워포인트 등에서 애니메이션 효과를 주게 된다면, 단순히 2D 회전을 하게 되면 부드럽게 효과가 적용되는 것을 볼 수 있지만, 3차원으로 회전 효과를 적용하면 영상이 끊기는 것을 볼 수 있습니다.

 

이 두 문제에 집중해 개선한 방법이 Axis-Angle 회전(rotation vector)인데요. 아래에서 간단하게 살펴보도록 하겠습니다.

 

 

Axis-Angle Rotation (Rotation vector)

---

축-각 회전(Axis-Angle rotation)은 오일러 각의 짐벌 락과 interpolation 제약 등을 어느 정도 해결했습니다. 그 이름에서도 직관적으로 알 수 있듯이 회전 변환을 회전축과 회전각을 이용해 표현한 방법인데요. 최종적으로 벡터 형태로 표현되기에 rotation vector로 불리기도 합니다. 또한, 처음 제안한 Rodrigues's rotation formula로 유도할 수 있어 로드리게스 회전이라고 부르기도 합니다.

 

Axis-Angle rotation

 

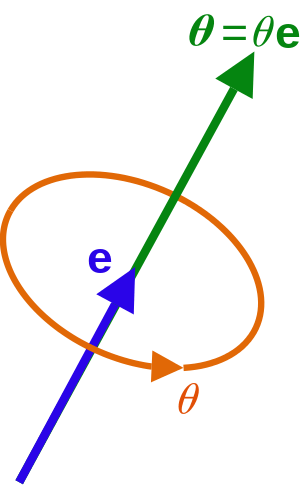
회전축을 나타내는 단위 벡터 $\mathbf{e}$와 회전각 $\theta$가 있을 때, 회전 벡터 $\mathbf{\theta}$는 방향은 $\mathbf{e}$, 크기는 $\theta$인 벡터($\mathbf{\theta}=\theta\mathbf{e}$)가 됩니다. 물리적 특징을 살펴보면, 임의의 축에 직교하는 평면에 대한 모든 회전을 표현할 수 있게 됩니다. 단일 벡터로 회전을 표현해 순서를 신경 쓸 필요가 없으며 짐벌 락에 빠질 위험도 적습니다 (없지는 않습니다).

 

그러나 Axis-Angle roation의 경우 연산량이 너무 방대해 회전이 중첩되는 경우 여러 트릭을 사용해야지 계산이 가능하다는 문제가 있습니다. 그래서 실전에서는 회전 벡터보다는 사원수(quarternion)를 많이 사용하고 있습니다. 따라서 복잡한 회전 벡터의 유도 과정은 잘 정리되어 있는 블로그 포스팅 소개로 대체하고자 하며, 결괏값을 소개하며 그 안에 내포된 의미를 살펴보고자 합니다.

 

$$\mathbf{R}=cos\theta \mathbf{I} + (1-cos\theta)\mathbf{nn}^T+sin\theta \mathbf{n}^{\wedge}$$

 

여기서 역으로 회전각 $\theta$를 유도하는 방법은 Axis-Angle rotation의 대각 성분의 합(trace, $tr$)을 통해 구할 수 있습니다.

 

$$tr(\mathbf{R})=cos\theta \  tr(\mathbf{I}) + (1-cos\theta)\ tr(\mathbf{nn}^T)+sin\theta \  tr(\mathbf{n}^{\wedge})$$

$$=3cos\theta + (1-cos\theta)=1+2cos\theta$$

$$\therefore \theta=arccos(\frac{tr(\mathbf{R})-1}{2})$$

 

위 식에서 $3 \times 3$ 단위 행렬($\mathbf{I}$)의 trace는 3이며, $\mathbf{nn}^T$의 경우 단위 벡터의 자기 자신과의 내적이기 때문에 1로 변하게 됩니다. 거기에 반대칭 행렬(skew-symmetric matrix)인 $\mathbf{n}^{\wedge}$의 경우 대각 성분의 합이 0입니다.

 

추가로, 회전축 $\mathbf{n}$은 회전 변환 후에도 아무것도 변하지 않게 됩니다. 즉, 아래와 같은 관계가 성립되게 되는데요.

 

$$\mathbf{Rn=n}$$

 

이 경우 $\mathbf{n}$이 $\mathbf{R}$의 eigen vector이며, eigen value는 1 임을 알 수 있습니다. 즉, 회전 벡터가 주어질 때 eigen decomposition 후 normalization 과정을 거치면 회전축을 구할 수 있게 됩니다.

 

 

Reference

---

모든 이미지에 대한 출처는 해당 이미지를 클릭하시면 열리도록 했습니다.

GitHub - gaoxiang12/slambook-en: The English version of 14 lectures on visual SLAM.