Introduction
우리가 흔히 보는 2D 영상 이미지에는 많은 변환 방법이 존재합니다. 강체 변환, 닮음 변환, Affine 변환 등 다양한 알고리즘이 존재하는데, 이는 본 포스트에서는 다루지 않을 예정입니다. SLAM에서 궁금한 부분은 3차원 공간에서 내가 어떻게 움직이고 있는지입니다. 즉, 3차원 공간에서 카메라가 어떻게 움직이고 있는지 구하는 게 최종 목표이며, 카메라는 크기가 변하거나 왜곡이 생기지 않습니다. 따라서 카메라를 하나의 강체(Rigid body)로 볼 수 있으며, 3D transform은 3D rigid body transform 문제로 요약됩니다. 이는 다른 말로 euclidean transform이라고 하며, 형태와 크기를 유지한 채로 위치(translation)와 회전(rotation)만 변할 수 있습니다.
이번 포스트는 이를 구하기 위해 알아야 할 사전 지식들을 정리했습니다. 위에서 잠시 언급한 2차원 변환 관련해서는 다크 프로그래머님의 포스트를 참고 부탁 드립니다.
Points, Vectors, Coordinates
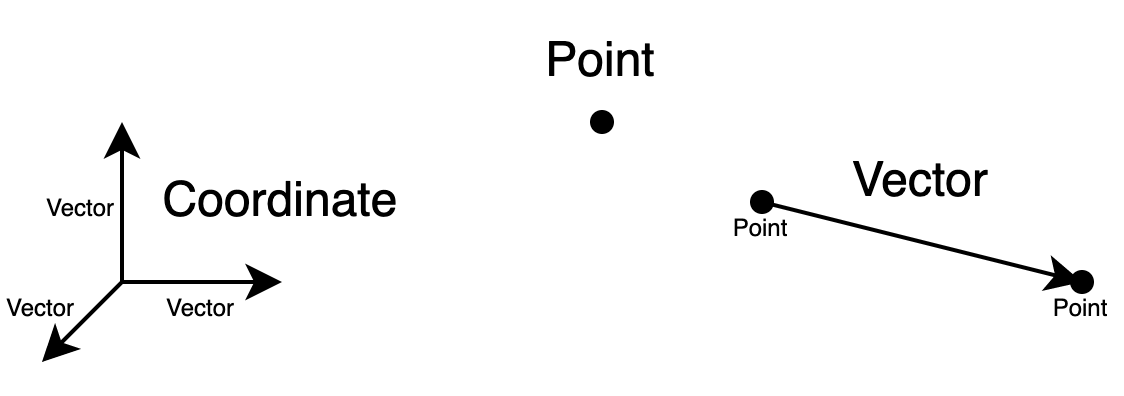
점(point)는 공간을 이루는 가장 기본적인 요소입니다. 부피(volume)도 없고, 길이(length)도 존재하지 않습니다. 그리고 점 2개가 모이면 벡터(vector)를 만들 수 있는데, 만드는 방법은 두 개를 이어주면 됩니다. 이때 출발점과 도착점이 구분되어 벡터는 방향 정보를 포함하게 됩니다. 벡터에서 중요한 점은 벡터의 좌표(coordinate)와 혼동하면 안 됩니다. 이게 도대체 무슨 소리일까요?
하나의 벡터는 공간 상에 유일합니다. 보통 굵은 소문자($\mathbf{a, b, c}$, etc)를 통해 표현되며, 벡터를 표기하기 위해서는 좌표를 포함한 어떠한 숫자가 필요하지 않습니다. 그러면 좌표계(coordinate system)는 무엇일까요? 좌표계는 점이나 벡터를 어떤 기준을 통해 표기하기 위한 기준 공간입니다. 보통 3개의 수직(orthogonal)을 이루는 벡터로 이루어져 있으며, 이 세 벡터를 기저 벡터(base)라고 합니다. 물론 기저 벡터들이 수직이 아닐 수 있지만, 그 경우 많은 고난과 역경을 거쳐야 하니 주의해 주세요. 아래는 $(\mathbf{e_1, e_2, e_3})$를 기저 벡터로 하는 좌표계에서 벡터 $\mathbf{a}$를 표현하는 방법입니다.
$$\mathbf{a}=[\mathbf{e_1, e_2, e_3}]\begin{bmatrix}
a_1 \\a_2
\\a_3
\end{bmatrix}=a_1\mathbf{e_1}+a_2\mathbf{e_2}+a_3\mathbf{e_3}$$
여기서 $(a_1, a_2, a_3)$이 벡터 $\mathbf{a}$의 좌표(coordinate)이며, 3차원을 표기하기 위해서 3개의 상수(scalar)가 필요함을 알 수 있습니다. 보다 직관적인 이해를 위해 아래 그림을 첨부했으니 참고 바랍니다.
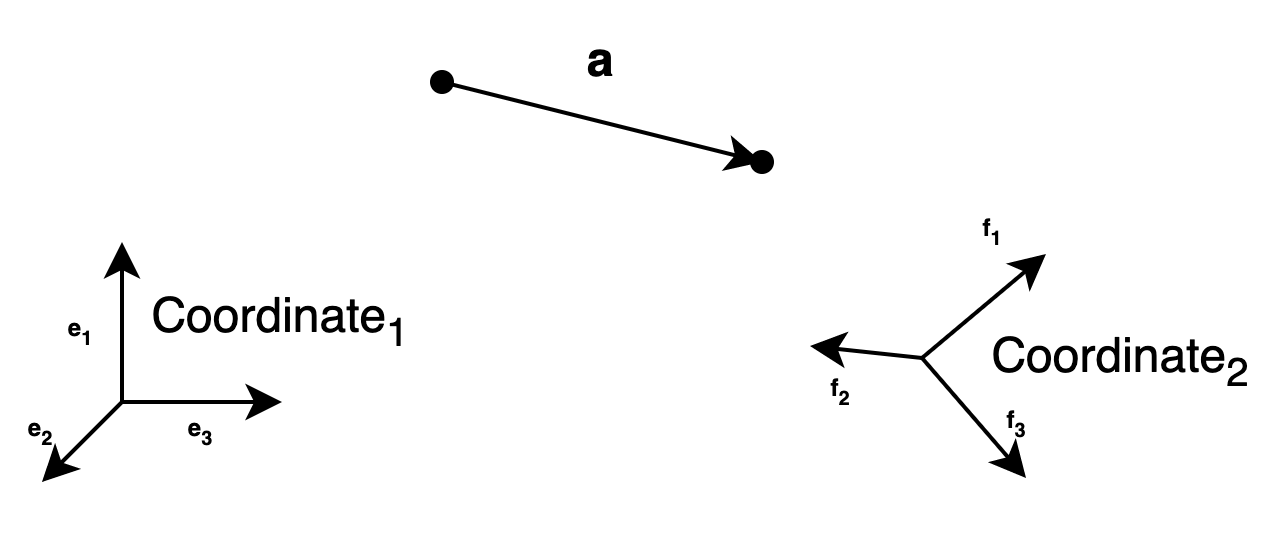
- Coordinate 1
$$\mathbf{a}=[\mathbf{e_1, e_2, e_3}]\begin{bmatrix}
a_1 \\a_2
\\a_3
\end{bmatrix}=a_1\mathbf{e_1}+a_2\mathbf{e_2}+a_3\mathbf{e_3}$$
- Coordinate 2
$$\mathbf{a}=[\mathbf{f_1, f_2, f_3}]\begin{bmatrix}
a_4 \\a_5
\\a_6
\end{bmatrix}=a_4\mathbf{f_1}+a_5\mathbf{f_2}+a_6\mathbf{f_3}$$
Inner/Outer Product
기본적으로 벡터에 대한 사칙 연산은 스칼라에 대한 사칙 연산과 같습니다. 그러나 내적(inner product)과 외적(outer product)의 경우 스칼라 연산에서는 볼 수 없는 형태입니다. 이번 챕터에서는 벡터의 내적과 외적의 풀이와 의미에 대해서 살펴보겠습니다.
두 벡터 $\mathbf{a,b}$의 내적(inner product)은 아래와 같이 풀 수 있습니다. 3차원 좌표계에서 표현된 두 벡터로 가정했습니다.
$$\mathbf{a \cdot b =a^T b} = \sum_{i=1}^3 \mathbf{a_i b_i = |a||b|}cos\theta$$
위 식에서 $\theta$는 $\mathbf{a,b}$ 사이의 각을 의미합니다. 두 벡터를 활용한 연산인 내적의 결괏값은 놀랍게도 스칼라인 것을 볼 수 있습니다. 여기에 내적은 추가로 두 벡터의 투영(projection) 관계를 내포하고 있는데요. 한 벡터를 다른 벡터에 정사영 시킨 길이를 다른 벡터의 길이와 곱해주는 것을 볼 수 있습니다. 그렇기 때문에 두 벡터 사이의 각이 $90^\circ $인 경우 내적의 결과는 0이 됩니다. 외적까지 설명한 후에 이해를 돕기 위해 그림을 첨부했으니 참고 바랍니다.
두 벡터 $\mathbf{a,b}$의 외적(outer product)은 아래와 같이 풀 수 있습니다. 3차원 좌표계에서 표현된 두 벡터로 가정했습니다.
$$\mathbf{a \times b}=\begin{Vmatrix}
\mathbf{e_1} & \mathbf{e_2} & \mathbf{e_3} \\
a_1 & a_2 & a_3 \\
b_1 & b_2 & b_3 \\
\end{Vmatrix}=\begin{bmatrix}
a_2b_3-a_3b_2 \\
a_3b_1-a_1b_3 \\ a_1b_2-a_2b_1
\end{bmatrix}=\mathbf{n|a||b|}sin\theta$$
위 식에서 $\theta$는 $\mathbf{a,b}$ 사이의 각을 의미하며, $\mathbf{n}$은 두 벡터에 모두 수직(orthogonal)인 단위 벡터를 의미합니다. 즉, 두 벡터에 대한 외적의 결괏값은 벡터로 나타나며, 방향은 두 벡터에 대한 법선 벡터(normal vector)이고 크기는 두 벡터로 만든 평행사변형의 넓이가 됩니다. 만약 두 벡터가 이루는 각이 $0^\circ$이면 법선 벡터를 형성할 수 없기에 외적의 결과값은 0이 됩니다. 이에 대한 이해를 돕기 위해 아래 그림을 첨부했으니 참고 바랍니다.
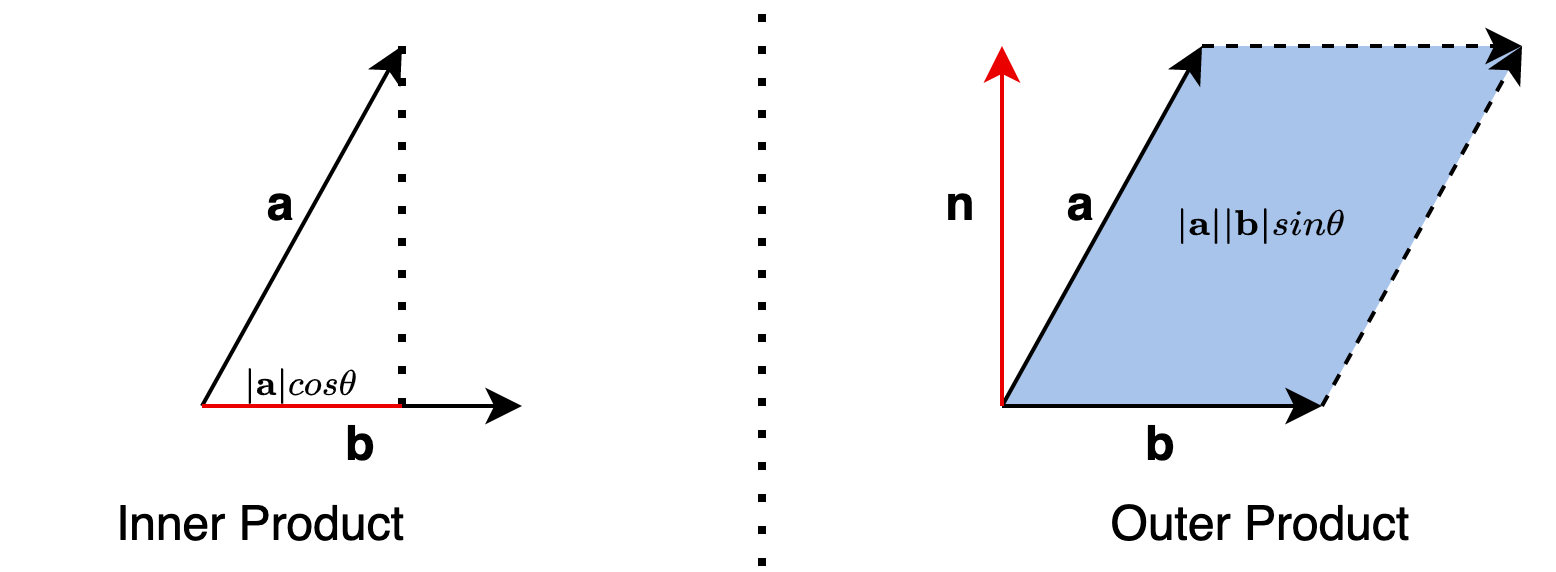
한편 외적에는 또 다른 중요한 의미가 있습니다. 위 외적에 대한 식을 아래와 같이 다르게 표현할 수 있습니다.
$$\begin{bmatrix}
0 & -a_3 & a_2 \\
a_3 & 0 & -a_1 \\
-a_2 & a_1 & 0 \\
\end{bmatrix}\mathbf{b} = \mathbf{a^\wedge b}$$
여기서 $\mathbf{a}$를 이용해 만든 행렬의 형태를 skew-symmetric matrix라고 합니다. 즉, 외적은 하나의 벡터 좌표(coordinate)로 skew-symmetric matrix와 다른 벡터를 곱한 결과와 같습니다. 이 변환이 중요한 이유는 non-linear operation을 linear operation으로 변환해 계산을 용이하게 만들었기 때문입니다. 이 트릭은 앞으로도 자주 등장할 예정이니 꼭 알아두시면 좋을 것 같습니다.
Reference
GitHub - gaoxiang12/slambook-en: The English version of 14 lectures on visual SLAM.
The English version of 14 lectures on visual SLAM. - GitHub - gaoxiang12/slambook-en: The English version of 14 lectures on visual SLAM.
github.com
