Intro
앞서 구했던 Optical Flow Constraint Equation(OFC)는 실제로 Optical Flow를 구하기에는 식이 부족했다. 미지수 2개, 식 1개로 방정식의 해를 특정할 수 없다. 그래서 우리는 가정을 추가해야 하는데 첫 번째 방법은 Lucas-Kanade Method이다. 추가된 Assumption, Optical Flow 계산, 장단점 순으로 글을 전개하겠다.
Assumption
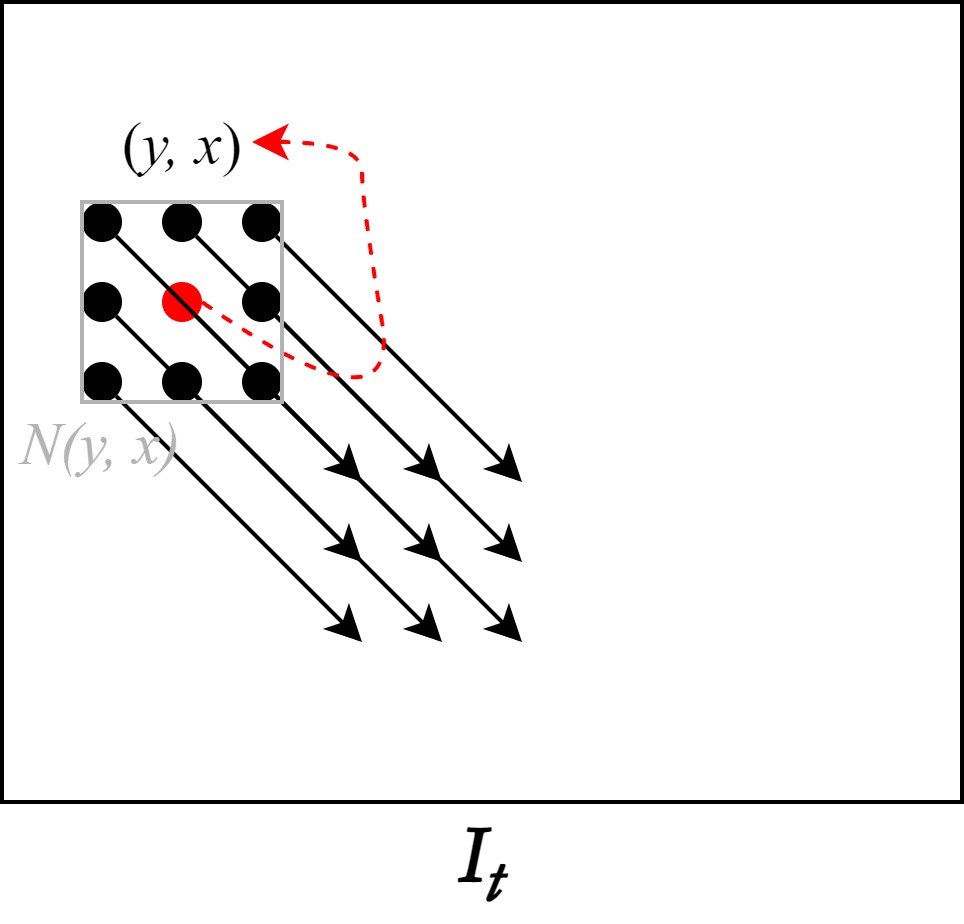
Lucas-Kanade Method에서 추가한 가정은 이 알고리즘의 특징을 잘 보여준다. 픽셀 (y, x)를 중심으로 생성한 nXn의 윈도우 N(y, x)의 Optical Flow는 같다. 즉, 윈도우 내부의 픽셀은 모두 같은 방향으로 움직이며, 이에 따라 Motion Vector 값이 같다. 이는 이 알고리즘이 지역적 방법으로 Optical Flow의 해를 찾음을 알 수 있다. 새로운 가정이 추가됨에 따라 Lucas-Kanade Algorithm 은 기존의 두 가지 가정에 더해 총 세 개의 가정을 가지게 된다.
- Brightness is constant
- Motion is Small
- Flow is essentially constant in a local neighborhood of the pixel
가정이 추가됨에 따라 OFC를 수정할 수 있다. 이때 Window Size는 N(y, x)에 속해 있는 픽셀의 수이다. 새로운 Assumption이 반영된 OFC는 아래와 같다.
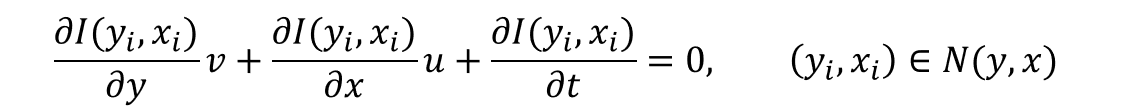
위 식을 행렬로 변환하기 위해 전개해보면 아래와 같이 쓸 수 있다. 아래 식에서 등장하지는 않지만 p를 Window의 중심점이라 하고, q는 p 인접 픽셀들이라 가정하자.
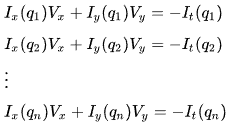
놀랍게도 2개의 미지수, 1개의 식으로 부족했던 기존의 OFC와 다르게 이번에는 식이 넘쳐난다. Window Size에 따라 n개의 식이 생기기 때문에 Optical Flow를 특정하는데 문제가 없다. 이제 위 식을 Av = b 형태의 행렬 계산으로 바꾸도록 하자.
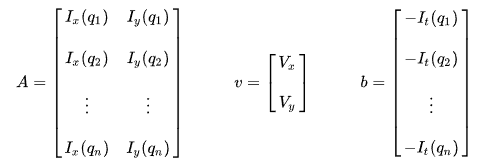
행렬로 변환하고 나니 필요한 수 대비 과도하게 많은 식이 더 직관적으로 보인다. 이제 이렇게 많은 식을 필요한 만큼만 남기기 위해 Least Squares Principle을 사용하자. 아래 식처럼 v에 대한 식으로 변환해 Motion Vector를 구할 수 있다.

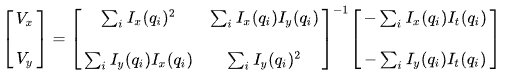
Pros and Cons
드디어 Optical Flow를 구하는 방법을 배워봤다. 그러나 Lucas-Kanade Method는 Optical Flow를 구하는 방법 중 One of Them에 불과하다. 기본적인 OFC에 서로 다른 가정을 추가함으로써 다양한 알고리즘을 만들 수 있다. 각각의 방법들은 서로 다른 장단점을 갖고 있으니 상황에 맞는 알고리즘을 선택하는 것이 중요할 것이다. 그렇다면 Lucas-Kanade의 장단점은 무엇일까? 우선 Window가 나왔으니 Computer Vision을 어느 정도 경험한 사람이면 즉각적으로 떠오르는 답이 있을 것이다. Window Size에 매우 종속적인 결과가 나온다! Window Size가 크면 연산은 빠른 대신 부정확할 것이며, 반대로 작으면 연산은 느리고 정확할 것이다. 정답이다. 나머지는 Optical Flow 관점에서 바라본 장단점이니 바로 떠오르지 않는다고 좌절할 필요는 없다. 모르는 게 당연하다.
- Pros
- Sparse Optical Flow에 속하며 Edge 등 Feature가 두드러지는 point를 사용해 연산량이 적다.
- Cons
- 윈도우 사이즈가 대체로 작은 편이라 윈도우보다 큰 움직임을 계산하지 못한다.
- 특정 점을 중심으로 Optical Flow를 계산하기 때문에 전역적으로 계산을 하는 Dense Optical Flow 대비 정확도가 낮다.
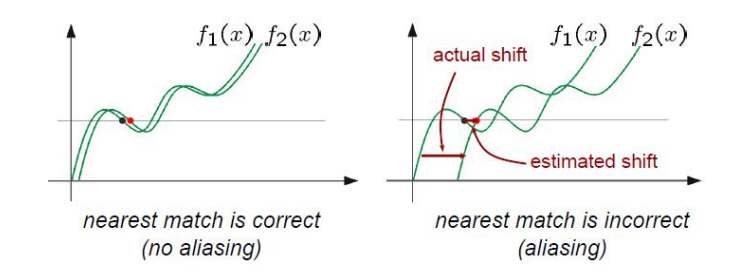
단점에서 이해하기 어려운 부분은 아마 윈도우보다 큰 움직임이 있을 때일 것이다. 움직임이 커도 그 값을 추적하면 되니 문제없는 것 아닌가요? 문제는 윈도우 기반 알고리즘은 윈도우 밖을 고려하지 않는다. 따라서 이 경우 Aliasing이 발생하게 되며 아래와 같이 왜곡이 발생하게 된다.
Next
이번 포스트에서는 Lucas-Kanade Algorithm에 추가된 Assumption을 이용해 Optical Flow를 어떻게 구하는지 알아봤다. 또한, LK의 장단점을 통해 이 역시 완벽한 방법은 아님을 알게 됐다. Algorithm Engineer들은 문제가 있을 경우 이를 개선하려고 노력한다. LK 역시 수많은 개선 아이디어가 있었다. 그중 Window를 사용하는 Algorithm에 공통적으로 등장하는 가중치를 통해 정확도를 올리는 방법과 Big Motion에 대응하기 위해 제안된 방법을 다음 포스트에서는 다뤄보겠다. 또한, 이번 포스트에서는 다루지 않은 Sparse Optical Flow의 고질적인 문제점에 대해서도 언급할 예정이다. 이 과정에서 앞서 언급됐던 개념이 확장되는 경험을 할 수 있을 것이다.
