Introduction
15654번: N과 M (5)
N개의 자연수와 자연수 M이 주어졌을 때, 아래 조건을 만족하는 길이가 M인 수열을 모두 구하는 프로그램을 작성하시오. N개의 자연수는 모두 다른 수이다. N개의 자연수 중에서 M개를 고른 수열
www.acmicpc.net
오늘 풀어볼 문제는 백준 15651번, N과 M (3)입니다. 자연수 N과 M이 주어질 때, 1부터 N까지의 자연수 중 중복을 허용하며 비내림차순으로 M개를 고른 수열을 모두 구하는 문제입니다. 입력과 출력은 아래와 같습니다. 비내림차순은 이름 그대로 오름차순이 아닌 수열을 의미합니다. 모든 원소가 같아도 괜찮지만 작아지면 안 됩니다. 이를 염두에 두고 풀어보도록 하겠습니다.
| 입력 | 자연수 N, M (1$\leq$M$\leq$N$\leq$8) , N 개의 서로 다른 자연수 ($\leq$10,000) |
| 출력 | ➡️ 한 줄에 하나씩 문제의 조건을 만족하는 수열을 출력한다 ➡️ 중복되는 수열을 여러 번 출력해서는 안된다 (숫자의 중복은 허용 X) ➡️ 각 수열은 공백으로 구분해서 출력해야 한다 ➡️ 수열은 사전 순으로 증가하는 순서로 출력해야 한다 |
이제 본격적으로 문제를 풀어보도록 하겠습니다. 글의 순서는 이번에는 source code를 먼저 보고, 어떤 사고의 흐름으로 계획을 짰는지 살펴보겠습니다. 그리고 ChatGPT에게 이번 문제를 풀어보게 할 예정입니다. Source code를 보고 싶어서 들어오신 분들을 위해서 순서를 조금 바꾸었습니다.
Source Code
/**
* @file q15654.cpp
* @author YoungJ-Baek (qordudwls1@gmail.com)
* @brief solution for BOJ #15654, https://www.acmicpc.net/problem/15654
* @version 0.1
* @date 2023-02-24
*
* @copyright Copyright (c) 2023
*
*/
#include <algorithm>
#include <iostream>
#include <vector>
#define MAX 9
using namespace std;
int input[MAX];
vector<int> result;
int visited[MAX];
int N, M;
void dfs(int count);
int main() {
cin >> N >> M;
for (int index = 0; index < N; index++) cin >> input[index];
sort(input, input + N);
dfs(0);
return 0;
}
void dfs(int count) {
if (count == M) {
for (auto iter = result.begin(); iter != result.end(); iter++)
cout << *iter << ' ';
cout << '\n';
} else {
for (int index = 0; index < N; index++)
if (visited[index] == true)
continue;
else {
visited[index] = true;
result.push_back(input[index]);
dfs(count + 1);
result.pop_back();
visited[index] = false;
}
}
}
Planning
우선 가능한 모든 조합을 찾아내는 문제인만큼 DFS(depth-first search) 기법을 활용하기로 결정했습니다. 또한, 중복은 허용하지 않는 만큼 `visited` 배열을 사용해 현재까지 선택된 숫자들을 추적했습니다. 여기에 재귀 함수를 이용해 목표에 도달할 때까지 모든 가능한 조합을 탐색했습니다.
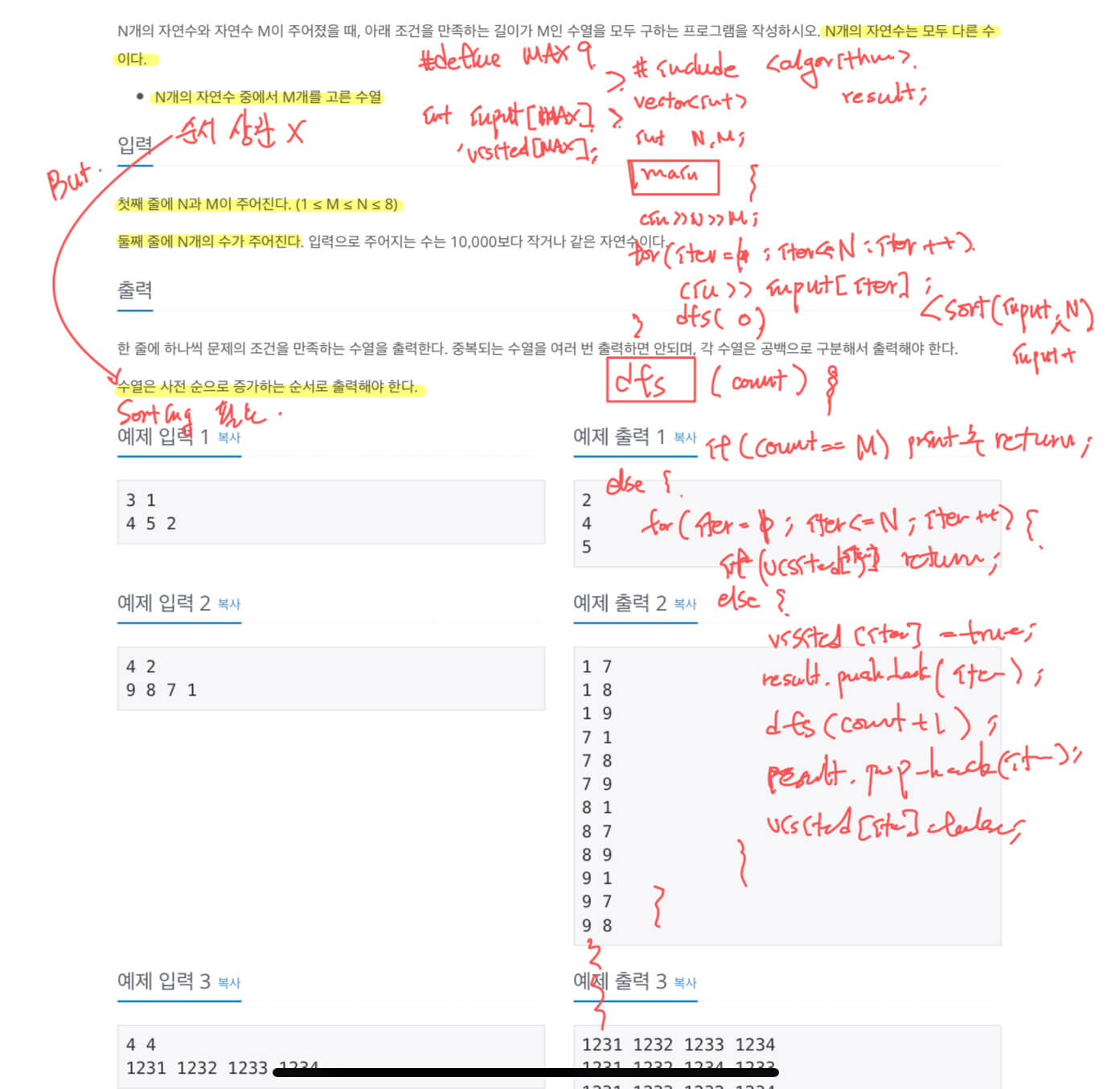
이 문제가 기존 문제와 다른 점은 주어진 자연수들이 sorting이 되어 있지 않을 수 있습니다. 기존에는 주어진 자연수들이 자연스럽게 오름차순으로 제공되었기에 별도로 sorting 하지 않았습니다. 그러나 이번 문제에서는 사전 순으로 증가하는 순서 조건을 만족하기 위해 별도로 algorithm library에서 제공하는 sort 함수를 사용했습니다. 아래는 아이패드에서 해당 문제를 풀기 위해 브레인 스토밍하는 과정입니다. 이런 방식은 나중에 기회가 된다면 좀 더 자세히 소개하도록 하겠습니다.
ChatGPT
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int n, m;
vector<int> nums, selected;
void dfs(int idx, int cnt) {
if (cnt == m) {
for (int i = 0; i < m; i++) {
cout << selected[i] << " ";
}
cout << '\n';
return;
}
for (int i = idx; i < n; i++) {
selected.push_back(nums[i]);
dfs(i, cnt + 1);
selected.pop_back();
}
}
int main() {
cin >> n >> m;
for (int i = 0; i < n; i++) {
int num;
cin >> num;
nums.push_back(num);
}
sort(nums.begin(), nums.end());
dfs(0, 0);
return 0;
}
Reference
GitHub - YoungJ-Baek/algorithm-study
Contribute to YoungJ-Baek/algorithm-study development by creating an account on GitHub.
github.com
Introduction
15654번: N과 M (5)
N개의 자연수와 자연수 M이 주어졌을 때, 아래 조건을 만족하는 길이가 M인 수열을 모두 구하는 프로그램을 작성하시오. N개의 자연수는 모두 다른 수이다. N개의 자연수 중에서 M개를 고른 수열
www.acmicpc.net
오늘 풀어볼 문제는 백준 15651번, N과 M (3)입니다. 자연수 N과 M이 주어질 때, 1부터 N까지의 자연수 중 중복을 허용하며 비내림차순으로 M개를 고른 수열을 모두 구하는 문제입니다. 입력과 출력은 아래와 같습니다. 비내림차순은 이름 그대로 오름차순이 아닌 수열을 의미합니다. 모든 원소가 같아도 괜찮지만 작아지면 안 됩니다. 이를 염두에 두고 풀어보도록 하겠습니다.
| 입력 | 자연수 N, M (1 , N 개의 서로 다른 자연수 ( |
| 출력 | ➡️ 한 줄에 하나씩 문제의 조건을 만족하는 수열을 출력한다 ➡️ 중복되는 수열을 여러 번 출력해서는 안된다 (숫자의 중복은 허용 X) ➡️ 각 수열은 공백으로 구분해서 출력해야 한다 ➡️ 수열은 사전 순으로 증가하는 순서로 출력해야 한다 |
이제 본격적으로 문제를 풀어보도록 하겠습니다. 글의 순서는 이번에는 source code를 먼저 보고, 어떤 사고의 흐름으로 계획을 짰는지 살펴보겠습니다. 그리고 ChatGPT에게 이번 문제를 풀어보게 할 예정입니다. Source code를 보고 싶어서 들어오신 분들을 위해서 순서를 조금 바꾸었습니다.
Source Code
/**
* @file q15654.cpp
* @author YoungJ-Baek (qordudwls1@gmail.com)
* @brief solution for BOJ #15654, https://www.acmicpc.net/problem/15654
* @version 0.1
* @date 2023-02-24
*
* @copyright Copyright (c) 2023
*
*/
#include <algorithm>
#include <iostream>
#include <vector>
#define MAX 9
using namespace std;
int input[MAX];
vector<int> result;
int visited[MAX];
int N, M;
void dfs(int count);
int main() {
cin >> N >> M;
for (int index = 0; index < N; index++) cin >> input[index];
sort(input, input + N);
dfs(0);
return 0;
}
void dfs(int count) {
if (count == M) {
for (auto iter = result.begin(); iter != result.end(); iter++)
cout << *iter << ' ';
cout << '\n';
} else {
for (int index = 0; index < N; index++)
if (visited[index] == true)
continue;
else {
visited[index] = true;
result.push_back(input[index]);
dfs(count + 1);
result.pop_back();
visited[index] = false;
}
}
}
Planning
우선 가능한 모든 조합을 찾아내는 문제인만큼 DFS(depth-first search) 기법을 활용하기로 결정했습니다. 또한, 중복은 허용하지 않는 만큼 `visited` 배열을 사용해 현재까지 선택된 숫자들을 추적했습니다. 여기에 재귀 함수를 이용해 목표에 도달할 때까지 모든 가능한 조합을 탐색했습니다.
이 문제가 기존 문제와 다른 점은 주어진 자연수들이 sorting이 되어 있지 않을 수 있습니다. 기존에는 주어진 자연수들이 자연스럽게 오름차순으로 제공되었기에 별도로 sorting 하지 않았습니다. 그러나 이번 문제에서는 사전 순으로 증가하는 순서 조건을 만족하기 위해 별도로 algorithm library에서 제공하는 sort 함수를 사용했습니다. 아래는 아이패드에서 해당 문제를 풀기 위해 브레인 스토밍하는 과정입니다. 이런 방식은 나중에 기회가 된다면 좀 더 자세히 소개하도록 하겠습니다.

ChatGPT
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int n, m;
vector<int> nums, selected;
void dfs(int idx, int cnt) {
if (cnt == m) {
for (int i = 0; i < m; i++) {
cout << selected[i] << " ";
}
cout << '\n';
return;
}
for (int i = idx; i < n; i++) {
selected.push_back(nums[i]);
dfs(i, cnt + 1);
selected.pop_back();
}
}
int main() {
cin >> n >> m;
for (int i = 0; i < n; i++) {
int num;
cin >> num;
nums.push_back(num);
}
sort(nums.begin(), nums.end());
dfs(0, 0);
return 0;
}
Reference
GitHub - YoungJ-Baek/algorithm-study
Contribute to YoungJ-Baek/algorithm-study development by creating an account on GitHub.
github.com
