Introduction
이전 게시물들을 통해 Image에서 Feature를 추출하는 방법을 알아봤습니다. Map을 만들기 위해서 연속된 Frame들에서 특징점을 추출한 후, Feature Matching (Tracking) 과정을 거쳐 특징점들의 변화를 추적합니다. 이번 포스트에서는 앞서 획득한 Feature들을 통해 Camera Pose Estimation을 수행하려 합니다. Camera Pose Estimation 과정은 가지고 있는 Feature의 특징 (차원)에 따라 차별점이 있는데요. 크게 아래 세 종류가 있으며, 이번 시리즈에서는 2D Image만 있을 때 사용 가능한 Epipolar Geometry에 대해서 알아보도록 하겠습니다.
- Epipolar Geometry: 2D 영상 데이터(2D, 2D)만 있을 때 활용 가능하며, Monocular에서 사용할 수 있어 Visual SLAM에서 주로 활용된다
- ICP (Iterative Closest Point): Depth 정보를 통해 3D 영상 데이터(3D, 3D)를 확보한 경우에 활용 가능하며, Binocular나 RGB-D 카메라에 적용 가능하다
- PnP (Perspective-n-Point): World 좌표계 기반 영상 데이터(3D)와 투영된 결과(2D)를 갖고 있을 때 보정된 Camera Pose를 계산하는 알고리즘이다
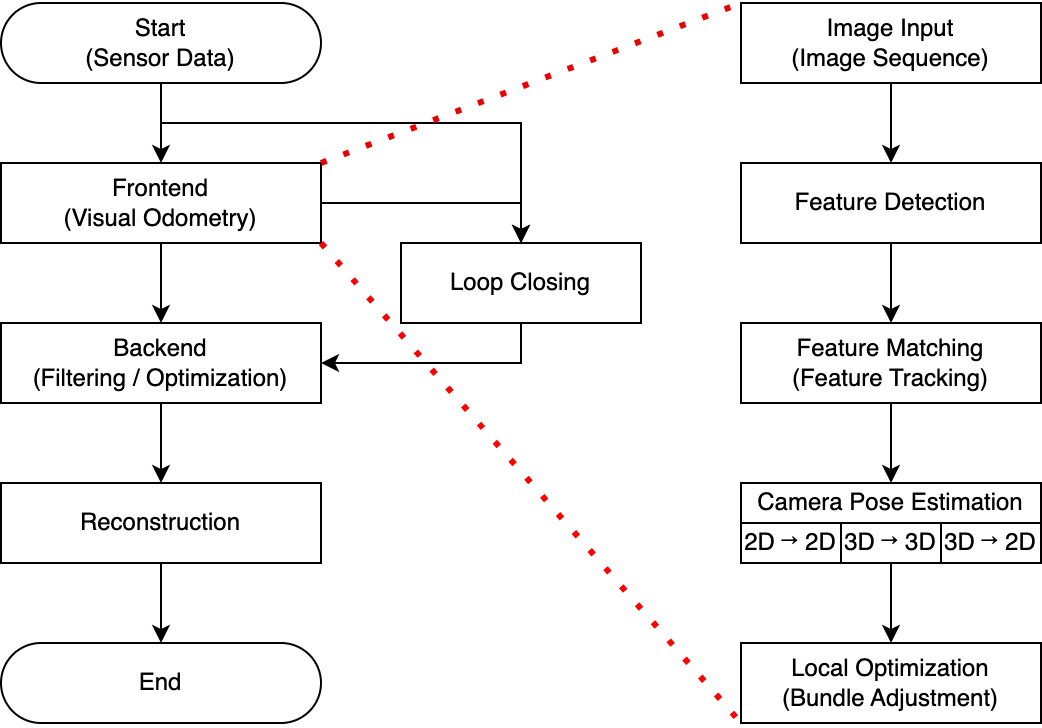
Epipolar Geometry
Epipolar Geometry는 동일한 사물/장면에 대해 서로 다른 두 지점에서 Image를 획득했을 때, 두 영상의 매칭쌍들에 대한 기하학적 관계를 나타냅니다. 말로만 들으면 감이 안 올텐데요. 아래 그림과 표를 통해 함께 살펴보도록 합시다.
Epipolar Geometry Concept Figure
Epipolar Geometry Terminologies
| Terminology | Description | Remark |
| $\mathbf{P(P')}$ | $Camera_1/Camera_2$에서의 Object 위치 | Camera Coordinates |
| $\mathbf{p(p')}$ | $Image_1/Image_2$에서 Object가 투영된 좌표, 투영점 | Pixel Coordinates |
| $\mathbf{O(O')}$ | $Camera_1/Camera_2$의 원점 | $\overrightarrow{\mathbf{OO'}}=Baseline$ |
| $\mathbf{e(e')}$ | Baseline과 Image Plane이 만나는 좌표 | Epihole |
| $\mathbf{l(l')}$ | 투영점($\mathbf{p, p'}$)과 Epihole을 이은 직선 | Epiline (Epipolar Line), Epipolar Plane과 Image Plane의 교선 |
| Epipolar Plane | $\mathbf{P(P')}$와 $\mathbf{O, O'}$가 속한 평면 |
위 그림과 표에서 알 수 있듯이 Epipolar Geometry는 서로 다른 두 이미지에서 픽셀의 관계를 나타냅니다. 또한, 이를 통해 SLAM에서는 카메라의 포즈를 추정하게 됩니다. 그렇다면 왜 카메라의 포즈나 Object의 위치를 특정하기 위해서는 꼭 2개의 이미지가 필요한 걸까요? 2 View Geometry라고도 불리는 Epipolar Geometry는 반드시 2개의 이미지가 필요합니다. 이 질문에 대한 답을 얻기 위해 한 번 반대로 생각해 보죠. 이미지가 한 개만 있다면 어떤 문제가 있을까요?
이미지가 한 개만 있는 경우 3차원의 물체를 2차원으로 투영하게 된다면, 차원 축소로 인해 정보의 손실이 발생합니다. 가장 대표적으로 Depth에 대한 정보를 상실하게 되죠. 그렇기 때문에 물체 $\mathbf{P}$의 위치를 특정하지 못합니다. 위 그림에서 $\overrightarrow{\mathbf{pP}}$의 모든 점이 $\mathbf{P}$의 위치가 될 가능성을 갖고 있습니다.
반면에 두 이미지를 사용하게 되면 많은 것들이 달라집니다. Feature matching을 통해 위 그림처럼 $\mathbf{P}$가 투영된 두 점 $\mathbf{p, p'}$의 위치를 안다고 가정해 봅시다. 그렇다면 우리는 $\overrightarrow{\mathbf{pP}}$와 $\overrightarrow{\mathbf{p'P}}$의 교점을 통해 $\mathbf{P}$의 위치를 특정할 수 있게 됩니다.
만약 Feature matching 과정이 부정확하거나 생략되어 $\mathbf{p'}$의 위치를 특정하지 못한 경우에도 할 수 있는 일이 있는데요. 비록 $\mathbf{P}$의 위치는 특정하지 못하지만, 반대로 $p'$의 위치가 Epipolar Line 내에 있음을 알려주는 단서가 됩니다. 우리는 Fundamental Matrix나 Essential Matrix를 통해 이런 것들을 해내는데요. 참고로 이 두 Matrix는 두 Pixel coordinate 사이에 성립하는 변환 행렬들이며, 후속 포스트에서 이를 다룰 예정입니다. Epipolar Geometry의 핵심은 이 두 Matrix가 항상 존재함을 증명하는 것에서부터 시작합니다. 이를 Epipolar Constraint라고 부르며, 지금부터는 이를 증명할 것입니다.
Epipolar Constraint
$\mathbf{P}$의 위치를 $\mathbf{P=[X,Y,Z]^T}$으로 정의하면, $\mathbf{p_1(p), p_2(p')}$은 아래와 같이 표현됩니다.
$$\mathbf{s_1p_1=KP, \quad s_2p_2=K(RP+t)}$$
여기서 $\mathbf{R, t}$는 $Image_1$에서 $Image_2$로의 변환을 의미하며, 이 둘은 알고 있다고 가정합니다. $\mathbf{K}$는 아시는 것처럼 Camera Intrinsic Parameter입니다. 위 식을 Homogeneous Coordinate 식을 사용해 표현하면 아래와 같이 표현할 수 있습니다. 그리고 계산을 좀 더 편하게 하기 위해 Normalized Plane에서 표현하도록 하겠습니다.
$$(Pixel Plane) \quad \mathbf{s_1p_1 \simeq p_1 \simeq KP, \quad s_2p_2 \simeq p_2 \simeq K(RP+t)}$$
$$(Normalized Plane) \quad \mathbf{x_1=K^{-1}p_1, \quad x_2=K^{-1}p_2}$$
식을 조금 다듬어 $\mathbf{x_2}$와 $\mathbf{x_3}$의 관계식을 만들어 봅시다.
$$\mathbf{Kx_2 \simeq K(RK^{-1}p_1+t) \simeq K(RK^{-1}Kx_1+t)}$$
$$\mathbf{x_2 \simeq Rx_1+t}$$
이제 양변에 $\mathbf{[t]_x}$를 취해줍니다. 이는 $\mathbf{t}$에 대한 Outer product와 같은 의미입니다.
$$\mathbf{[t]_x x_2 \simeq [t]_x (Rx_1+t)}$$
$$\mathbf{ [t]_x x_2 \simeq [t]_x Rx_1 }, \quad \because \mathbf{ [t]_x t = |t|^2sin(\theta)\overrightarrow{n} }=0$$
식을 더 간단하게 만들어 봅시다. 자고로 한 변이 0이 되어야 Constraint 식이라고 할 수 있죠. 양변에 $left \mathbf{x_2^T}$를 inner product 해줍시다.
$$\mathbf{x_2^T \cdot ([t]_x x_2) \simeq x_2^T \cdot [t]_x Rx_1}$$
$$\mathbf{x_2^T \cdot [t]_x Rx_1 = 0}$$
여기서는 $\mathbf{[t]_x x_2}$는 $\mathbf{t, x_2}$ 모두와 직교합니다. 즉, 여기에 $\mathbf{x_2}$를 내적하게 되면 0이 되어 식이 간단해지죠. 이렇게 Normalized Coordinate에서의 Epipolar Constraint를 구해봤습니다. 이를 Pixel Coordinate 기준으로 바꾸면 아래와 같습니다.
$$\mathbf{K^{-T}p_2^T [t]_xRK^{-1}p_1=0}$$
Next
이번 포스트에서는 Epipolar Geometry에 대해 소개하고 그 근간을 이루는 Epipolar Constraint를 유도했습니다. 그런데 이걸 왜 구한 걸까요? 다음 포스트에서는 그 답을 줄 Fundamental Matrix와 Essential Matrix를 소개하도록 하겠습니다.
Introduction
이전 게시물들을 통해 Image에서 Feature를 추출하는 방법을 알아봤습니다. Map을 만들기 위해서 연속된 Frame들에서 특징점을 추출한 후, Feature Matching (Tracking) 과정을 거쳐 특징점들의 변화를 추적합니다. 이번 포스트에서는 앞서 획득한 Feature들을 통해 Camera Pose Estimation을 수행하려 합니다. Camera Pose Estimation 과정은 가지고 있는 Feature의 특징 (차원)에 따라 차별점이 있는데요. 크게 아래 세 종류가 있으며, 이번 시리즈에서는 2D Image만 있을 때 사용 가능한 Epipolar Geometry에 대해서 알아보도록 하겠습니다.
- Epipolar Geometry: 2D 영상 데이터(2D, 2D)만 있을 때 활용 가능하며, Monocular에서 사용할 수 있어 Visual SLAM에서 주로 활용된다
- ICP (Iterative Closest Point): Depth 정보를 통해 3D 영상 데이터(3D, 3D)를 확보한 경우에 활용 가능하며, Binocular나 RGB-D 카메라에 적용 가능하다
- PnP (Perspective-n-Point): World 좌표계 기반 영상 데이터(3D)와 투영된 결과(2D)를 갖고 있을 때 보정된 Camera Pose를 계산하는 알고리즘이다

Epipolar Geometry
Epipolar Geometry는 동일한 사물/장면에 대해 서로 다른 두 지점에서 Image를 획득했을 때, 두 영상의 매칭쌍들에 대한 기하학적 관계를 나타냅니다. 말로만 들으면 감이 안 올텐데요. 아래 그림과 표를 통해 함께 살펴보도록 합시다.
Epipolar Geometry Concept Figure

Epipolar Geometry Terminologies
| Terminology | Description | Remark |
| Camera Coordinates | ||
| Pixel Coordinates | ||
| Baseline과 Image Plane이 만나는 좌표 | Epihole | |
| 투영점( |
Epiline (Epipolar Line), Epipolar Plane과 Image Plane의 교선 |
|
| Epipolar Plane |
위 그림과 표에서 알 수 있듯이 Epipolar Geometry는 서로 다른 두 이미지에서 픽셀의 관계를 나타냅니다. 또한, 이를 통해 SLAM에서는 카메라의 포즈를 추정하게 됩니다. 그렇다면 왜 카메라의 포즈나 Object의 위치를 특정하기 위해서는 꼭 2개의 이미지가 필요한 걸까요? 2 View Geometry라고도 불리는 Epipolar Geometry는 반드시 2개의 이미지가 필요합니다. 이 질문에 대한 답을 얻기 위해 한 번 반대로 생각해 보죠. 이미지가 한 개만 있다면 어떤 문제가 있을까요?
이미지가 한 개만 있는 경우 3차원의 물체를 2차원으로 투영하게 된다면, 차원 축소로 인해 정보의 손실이 발생합니다. 가장 대표적으로 Depth에 대한 정보를 상실하게 되죠. 그렇기 때문에 물체
반면에 두 이미지를 사용하게 되면 많은 것들이 달라집니다. Feature matching을 통해 위 그림처럼
만약 Feature matching 과정이 부정확하거나 생략되어
Epipolar Constraint
여기서
식을 조금 다듬어
이제 양변에
식을 더 간단하게 만들어 봅시다. 자고로 한 변이 0이 되어야 Constraint 식이라고 할 수 있죠. 양변에
여기서는
Next
이번 포스트에서는 Epipolar Geometry에 대해 소개하고 그 근간을 이루는 Epipolar Constraint를 유도했습니다. 그런데 이걸 왜 구한 걸까요? 다음 포스트에서는 그 답을 줄 Fundamental Matrix와 Essential Matrix를 소개하도록 하겠습니다.
