Introduction
앞서 Epipolar Geometry를 소개하며 2D-2D feature를 이용한 포즈 추정 방법을 알아보았습니다. 그러나 2D 이미지만을 가지고 포즈 추정을 하게 되면 필연적으로 오차가 생길 수밖에 없으며, 속도 또한 정확도 대비 느리다는 문제가 있습니다. 그렇기에 monocular 카메라를 사용해야만 하는 상황이 아니라면 RGB-D, stereo vision을 사용하거나 좀 돈이 많은 곳은 라이다(lidar)를 사용해 정교한 정보들을 추출합니다.
더 많은 정보가 있을 때 우리는 어떻게 포즈를 추정할 수 있을까요? 앞선 포스트에서 2D-2D, 3D-2D, 3D-3D feature가 있을 때 각각 어떠한 방법을 사용해야하는지 소개했는데요. 오늘은 3D point cloud와 2D feature point를 갖고 있을 때 포즈를 추정하는 PnP (Perspective n Points) 알고리즘을 소개하려고 합니다. 이번 시리즈는 PnP와 ICP를 간단하게 다루는 정도로 끝내려 하는데요. 현재 스터디 팀에서 실제 PnP와 ICP를 구현해 보는 중이니 자세한 내용은 나중에 다루려고 합니다.
Perspective n Points
Perspective n Points (a.k.a. PnP) 알고리즘은 3D point cloud 정보와 2D feature point 정보를 알고있을 때 카메라의 포즈를 구하는 알고리즘입니다. 2D feature point 만을 가지고 포즈를 구하는 epipolar geometry의 경우 최소 8개 (non-linear의 경우 5개)의 feature point를 필요로 했습니다. 또한, 순수 회전에 취약하고, 초기화 과정을 필요로 함과 동시에 스케일 문제가 해소되지 않았죠. PnP는 최소 3개의 점에 대한 3D-2D 매칭 정보만 있으면 카메라의 포즈를 추정할 수 있습니다. 여기에 검증(verification)용으로 1개의 특징쌍이 추가로 필요하지만 포즈 추정에는 3개만 있으면 이론적으로 구할 수 있습니다.
3D 정보를 쉽게 구할 수 있는 binocular(stereo vision)이나 RGB-D 카메라에서 많이 사용됩니다. 또한, monocular 카메라에서도 epipolar geometry를 이용해 초기화 후 PnP를 통해 이후 연산을 진행하기도 합니다. 번거롭더라도 이런 방식을 취하는 이유는 PnP는 별도의 초기화 과정이나 epipolar constraints 없이 더 적은 정보로 더 좋은 결과를 얻을 수 있기 때문인데요. 이런 PnP 알고리즘은 방법에 따라 P3P, DLT, EPnP, UPnP 등 많은 방법이 있습니다. 이번 포스트에서는 가장 기본적인 DLT와 P3P를 다루도록 하겠습니다.
Direct Linear Transform
Direct Linear Transform (a.k.a. DLT)는 PnP 문제를 푸는 가장 무식한 방법입니다. 3차원 좌표 $P_1(X_1,Y_1,Z_1,1)$와 이를 투영한 2차원 좌표 $x_1(u_1,v_1,1)가 있을 때 두 좌표의 관계식은 아래와 같습니다. 편의상 모두 homogeneous 좌표로 표현했습니다.
$$s_1\begin{pmatrix}
u_1 \\
v_1 \\1
\end{pmatrix}=\underbrace{\begin{pmatrix}
t_1 & t_2 & t_3 & t_4 \\
t_5 & t_6 & t_7 & t_8 \\
t_9 & t_{10} & t_{11} & t_{12} \\
\end{pmatrix}}_{[\mathbf{R|t}]}\begin{pmatrix}
X_1 \\
Y_1 \\
Z_1 \\1
\end{pmatrix}$$
위 식에서의 변환식은 우리가 알고 있는 Transformation matrix $T$가 아닙니다. 정확한 용어가 있는 것은 아니나, $R, t$의 곱 혹은 $R, t$의 encoding matrix라고 생각하시면 됩니다. 다시 돌아와 위 식을 정리하면 아래와 같이 표현할 수 있습니다.
$$\left\{\begin{matrix}
s_1u_1=t_1X_1+t_2Y_1+t_3Z_1+t_4 \\
s_1v_1=t_2X_1+t_6Y_1+t_7Z_1+t_8 \\s_1=t_9X_1+t_{10}Y_1+t_{11}Z_1+t_12
\end{matrix}\right.$$
이 식을 $u_1, v_1$에 대해 정리하면 아래와 같습니다.
$$u_1=\frac{t_1X_1+t_2Y_1+t_3Z_1+t_4}{t_9X_1+t_{10}Y_1+t_{11}Z_1+t_{12}}, \quad v_1=\frac{t_5X_1+t_6Y_1+t_7Z_1+t_8}{t_9X_1+t_{10}Y_1+t_{11}Z_1+t_{12}}$$
이제 변환 행렬 $\mathbf{[R|t]}$를 행벡터(row vector) $\mathbf{t_1,t_2,t_3}$으로 나누어 표현을 간소화하겠습니다.
$$\mathbf{t_1}=[t_1,t_2,t_3,t_4]^T,\ \mathbf{t_2}=[t_5,t_6,t_7,t_8]^T,\ \mathbf{t_3}=[t_9,t_{10},t_{11},t_{12}]^T$$
$$\left\{\begin{matrix}
\mathbf{t_1}P_1-\mathbf{t_3}P_1u_1=0 \\ \mathbf{t_2}P_1-\mathbf{t_3}P_1v_1=0
\end{matrix}\right.$$
이제 하나의 3D-2D 상관관계를 통해 선형방정식 2개를 얻었습니다. 총 12개의 변수($t_1~t_{12}$)를 구해야 하기 때문에 최소 6개의 상관관계가 필요합니다. 보통의 문제에서는 매칭쌍이 12개보다 훨씬 많기 때문에 SVD를 활용해 least-squared solution을 구하곤 합니다.
$$\begin{pmatrix}
P_1^T & 0 & -u_1P_1^T \\
0 & P_1^T & -v_1P_1^T \\
\vdots & \vdots & \vdots \\
P_N^T & 0 & -u_NP_N^T \\
0 & P_N^T & -V_NP_N^T \\
\end{pmatrix}\begin{pmatrix}
\mathbf{t_1} \\
\mathbf{t_2} \\ \mathbf{t_3}
\end{pmatrix}=0$$
P3P
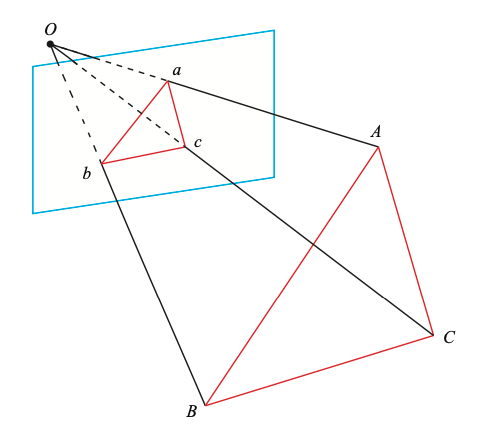
P3P 알고리즘은 쉽게 말하면 점 3개를 활용해 카메라의 $\mathbf{R, t}$를 구하는 방법입니다. 앞서 소개한 DLT가 최소 6개의 점이 필요한 반면, P3P는 최소 3개 (+ 검증용 1개)가 필요해 훨씬 간편한 방법입니다. 물론 여기서 1개가 매칭되는 (3D, 2D) 쌍임을 생각하면 마냥 구하기 쉬운 건 아니겠죠. 아무튼 준비물이 다 마련되면 아래와 같은 기하학적 관계가 성립함을 알 수 있습니다.
여기서 3차원 좌표 $A,B,C$는 월드 좌표계의 점이며, $a,b,c$는 이미지 평면에 투영된 2차원 좌표들입니다. 카메라의 원점 $O$와 각 좌표들로 만든 삼각형은 아래와 같은 닮음 관계를 갖고 있습니다.
$$\triangle Oab \sim \triangle OAB,\quad \triangle Obc \sim \triangle OBC,\quad \triangle Oca \sim \triangle OCA$$
이제 cosine 법칙을 위 삼각형들에 적용해 봅시다. 참고로 저는 cosine 법칙이 기억이 안 나서 구글링을 통해 찾아봤습니다. 저와 같은 분들이 계실 수 있어 아래에 접은 글로 해당 내용을 첨부했습니다.

$$a^2=b^2+c^2-2bc\cos{A}$$
$$b^2=c^2+a^2-2ca\cos{B}$$
$$c^2=a^2+b^2-2ab\cos{C}$$
$$\overline{AB}^2=\overline{OA}^2+\overline{OB}^2-2\overline{OA}\cdot\overline{OB}\cos{<a,b>}$$
$$\overline{BC}^2=\overline{OB}^2+\overline{OC}^2-2\overline{OB}\cdot\overline{OC}\cos{<b,c>}$$
$$\overline{CA}^2=\overline{OC}^2+\overline{OA}^2-2\overline{OC}\cdot\overline{OA}\cos{<c,a>}$$
이제부터는 위 식을 정리하는 과정입니다. 우선 $\overline{OC}^2$으로 모든 식을 나눠준 후, $x=\overline{OA}/\overline{OC}$,$\ y=\overline{OB}/\overline{OC}$,$\ v=\overline{AB}^2/\overline{OC}^2$, $u=\overline{BC}^2/\overline{AB}^2$, $w=\overline{AC}^2/\overline{AB}^2$을 이용해 정리합니다.
$$x^2+y^2-2xy\cos{<a,b>}=v$$
$$y^2+1^2-2y\cos{<b,c>}-uv=0$$
$$x^2+1^2-2x\cos{<c,a>}-wv=0$$
첫 번째 식의 $v$를 나머지 두 식에 대입해 주면 아래와 같은 식을 구할 수 있습니다.
$$(1-u)y^2-ux^2-2y\cos{<b,c>}+2uxy\cos{<a,b>}+1=0$$
$$(1-w)x^2-wy^2-2x\cos{<c,a>}+2wxy\cos{<a,b>}+1=0$$
과연 여기서 구해야 할 값은 무엇일까요? 우선 카메라의 원점$O$와 이미지 평면의 세 좌표 $a,b,c$는 모두 알고 있기에 cosine들($\cos{<a,b>}$, $\cos{<b,c>}$, $\cos{<c,a>}$은 모두 알고 있는 값이 됩니다. 또한 월드 좌표계의 세 점 $A,B,C$ 역시 모두 알고 있기 때문에 $u,w$모두 상수로 표현됩니다. 반면에 $x,y$는 카메라 좌표계에서 바라본 세 점 $A,B,C$이기 때문에 카메라가 이동함에 따라 변하게 됩니다. PnP는 바로 이러한 $x,y$, 즉 카메라의 포즈를 구하는 알고리즘입니다.
두 개의 미지수와 두 개의 방정식이기 때문에 이 문제를 풀 수 있는데요. 하지만 $x,y$ 모두 $+,-$ 부호를 모두 취할 수 있기 때문에 총 4개의 가능한 해가 존재합니다. 여기서 최적의 해를 찾기 위해 네 번째 매칭쌍이 필요하게 됩니다. 물론 P3P 알고리즘에서 매칭쌍이 네 개가 필요한 것은 말이 안 된다고 할 수 있으며, 이 경우 orientation을 알 수 있는 다른 센서 정보를 활용해 최적의 해를 구하도록 합니다.
Conclusion
PnP 알고리즘을 통해 카메라 좌표계에서의 3D 오브젝트의 좌표를 구할 수 있었습니다. 이 경우 월드 좌표계에서의 3D 오브젝트와 비교가 가능한데요. 3D-2D 문제가 이제는 3D-3D 포즈 추정 문제로 변화했음을 알 수 있습니다. 이 경우 적용할 수 있는 알고리즘이 다음 포스트에서 소개할 ICP (Iterative Closest Point) 알고리즘입니다.
또한, PnP 알고리즘은 3개의 점만으로도 카메라의 포즈를 추정할 수 있는 알고리즘으로 높은 효율성을 자랑함을 이번 포스트에서 살펴볼 수 있었습니다. 물론 오직 3개의 점만을 사용하기 때문에 알고리즘에 사용하는 점들이 노이즈에 노출되거나 왜곡이 발생하면 정확도가 급격하게 떨어지는 단점이 있으며, 점들이 많은 경우 오히려 탐색에 어려움을 겪기도 하지만 여전히 강력한 알고리즘이라고 볼 수 있습니다. 실제로 EPnP나 UPnP에서는 iteration을 돌면서 노이즈를 제거하며 최적값에 근사해가는 방법을 택했습니다.
Reference
GitHub - gaoxiang12/slambook-en: The English version of 14 lectures on visual SLAM.
The English version of 14 lectures on visual SLAM. - GitHub - gaoxiang12/slambook-en: The English version of 14 lectures on visual SLAM.
github.com